탐욕 알고리즘, 역추적 알고리즘, 분기 한정법을 다뤄오면서 공통적으로 나왔던 0-1 배낭 문제를 기억하는지 모르겠다. 역추적 알고리즘 글에서 이 문제가 NP 문제라고 했다. 본인도 이해하기 굉장히 어려운 개념이었는데(아직도 제대로 이해한 것 같지는 않다 ㅠㅠ😥) 이번 글에서는 이 NP 문제에 대해 다뤄볼 것이다. 이번 글에서 알아볼 사항들은 다음과 같다.
- tractable/intractable(다루기 쉬운/다루기 어려운) 문제 분류
- 결정 문제 정의
- class P 정의
- 비결정적 문제 정의
- class NP 정의
- 다항식 변환 정의
- NP-Complete class 정의
Polynomial Time Algorithm?
우선 다항 시간 알고리즘에 대해 이해해보자. 이는 worst-case 시간 복잡도가 입력 크기 n에 대한 다항 함수로 구성되는 알고리즘이다. 우리가 이전까지 흔히 볼 수 있던 형식의 시간 복잡도가 이것이다. 즉 \(T_{w}(n)=O(p(n))=O(n^k),k\geq 0\)이다. 예를 들어보자.
- Ex 1) \(2n, 3n^3+4n, n^{10}+5n, nlogn(< n^2) \)은 다항 시간 알고리즘이다.
- Ex 2) \(2^n, 2^{0.01n}, 2^{\sqrt{n}}, n!\)은 다항 시간 알고리즘이 아니다.
Solvable Problem vs. Unsolvable Problem
이번에는 컴퓨터로 해결할 수 있는 문제와 해결할 수 없는 문제는 어떻게 구별할 수 있을지 알아보자.
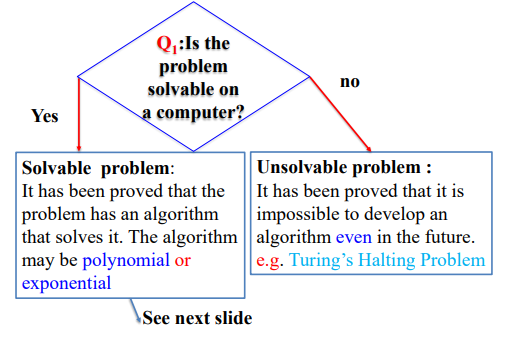
컴퓨터가 해결할 수 있는 문제는 주어진 문제에 대해 해결할 수 있는 알고리즘이 입증되어있다. 해당 알고리즘은 다항 또는 지수 시간 복잡도를 가진다.
해결할 수 없는 문제는 미래에도 해당 문제에 대한 해결 알고리즘을 개발하는게 불가능하다는 것이 증명된 문제들이다. 예를 들어 튜링의 정지 문제가 있다.
Tractable Problem vs. Intractable Problem
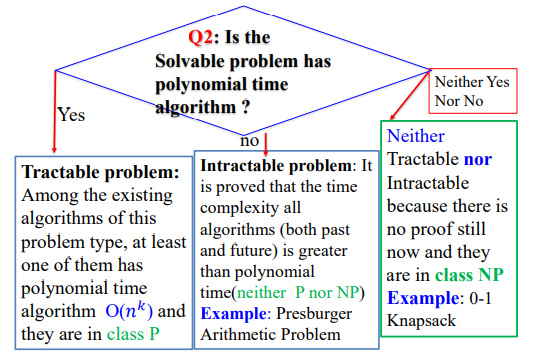

이번에는 다루기 쉬운(tractable), 다루기 어려운 문제(intractable)에 대해 알아보자. 우선 tractable 문제는 해당 문제 유형의 기존 알고리즘 중 적어도 하나는 다항 시간 알고리즘 \(O(n^k)\)을 가지고 class P에 속하는 문제이다.
intractable 문제는 해당 문제 유형의 모든 알고리즘(과거 및 미래 모두)이 다항 시간보다 시간 복잡도가 더 크다는(P도 NP도 아니다) 것이 증명된 문제들(ex. Presburger 산술 문제)이다.
이외에 아직 증거가 없고 NP class에 속하기 때문에 tractable도 intractable도 아닌 문제들이 존재한다. 이에 대한 예시는 우리가 많이 했었던 0-1 배낭 문제가 있다. 즉 현재까지 적어도 하나의 다항 시간 알고리즘이 발견되지 않았고 미래에 다항 시간 알고리즘을 개발하는게 불가능하다는 것이 증명된 적이 없다. 그러므로 미래에 다항 시간 알고리즘은 개발될 수도, 개발되지 않을 수도 있다.
여기서 intractability(난해성)은 주어진 문제를 해결하는 알고리즘의 속성이 아닌 문제 고유의 속성이다. 그렇다면 주어진 문제에 대해 한 알고리즘 개발자가 해당 문제에 대한 비다항 시간 알고리즘을 찾았다면 이 문제가 intractable한 문제라고 말할 수 있을까? 정답은 No이다. 그러므로 계산 복잡도 이론의 주요 목적은 문제의 고유한 난이도에 따라 문제를 분류하는 것이다.
일부 문제들은 비다항 개수만큼의 출력을 필요로 하기 때문에 다루기 힘든 문제들이다. 따라서 필요한 출력 수가 합리적이지 않고 문제의 정의가 비현실적이다. 예를 들어 완전히 연결된 그래프의 해밀턴 경로(위키)를 결정하는 것은 다루기 어려운 문제이다. 왜냐하면 그래프의 경로 수가 (n-1)!이기 때문이다.
The Theory of NP
- 결정 문제: yes or no 형식의 답을 요구하는 문제
- 최적화 문제: 답의 경우의 수가 무한, 가장 좋은 해를 요구하는 문제
우리는 이전에 동적, 역추적 및 분기 한정법 알고리즘을 알아봤었는데 0-1 배낭 문제, 부분 집합 합 문제, 해밀턴 경로 문제와 같이 tractable하지도 않고 intractable 하지도 않은 문제 사이에는 어떠한 관계가 있다. 따라서 NP 이론은 이러한 문제 유형 간의 관계를 발전시키는데 중점을 둔다.
결정 문제만으로 연구를 제한하는 것이 NP 이론을 발전시키기 쉽기 때문에 최적화 문제 대신 결정 문제만 사용하여 NP 이론을 개발한다. 결정 문제는 yes or no의 두 가지 가능한 결과만 있다. 그리고 각 최적화 문제에는 해당하는 결정 문제들이 있다. 또한 미래에서 문제에 대한 다항 시간 알고리즘을 개발하면 해당 최적화 문제에 대한 다항 시간 알고리즘도 얻을 수 있음이 입증되었다.
Optimization Problems and their Corresponding Decision Problems
각 최적화 문제에 해당하는 결정 문제들이란 무엇일까? 예시를 통해 이해해보자.
Ex 1. 외판원 최적화 문제: 가중 방향 그래프가 주어졌을 때 한 노드에서 시작하여 다른 모든 노드를 한 번씩만 방문한 다음 시작 노드에서 끝이나는 경로 중 총 가중치의 값이 최소인 경로를 결정하는 문제이다. 해당 문제에 대한 출력은 스칼라 값(최소 경로의 길이) 및 벡터 수량(최소 경로를 따라가는 노드 목록)이다. 그렇다면 이 문제에 해당하는 결정 문제는 '주어진 가중 방향 그래프와 양수 D(스칼라 수량)에 대해 길이가 D이하인 경로가 있는지'이다.
Ex 2. 0-1 배낭 문제: 문제에 대한 설명은 생략하겠다. 이 문제에 해당하는 결정 문제는 '주어진 무게 W, 이익 P에 대해 '(총 무게) <= W', '(총 이익) >= P'가 되도록 배낭에 물건을 싣는 것이 가능한지'이다.
Properies of Combinative and Permutation Based Decision Problems
조합 및 순열 결정 문제에는 다음과 같은 두가지 공통된 특징이 있다.
- 해를 선택해야 하는 입력 크기에 대한 함수는 가능한 옵션이 기하급수적으로 많다.
- 이를 해결하기 위한 다항 시간 알고리즘을 개발하는 것은 어렵지만 무작위로 생성된 해의 유효성은 다항 시간에서 검증할 수 있다.
- 무작위 해는 컴퓨터에 의해 무작위 문자열로 생성될 수 있다. 이것은 비결정적 알고리즘의 정의로 이어진다.
Non-Deterministic Algorithm
비결정적 알고리즘은 결정 문제의 특정 입력 입력 인스턴스를 취하고 무작위 추측으로 해를 생성(1. 추측 단계)하고 결정론적 알고리즘을 사용하여 무작위로 생성된 해의 정확성을 검증(2. 검증 단계)한다.
(1): 추측 단계에서 임의의 문자열 S는 주어진 입력 인스턴스에 대한 후보 솔루션으로 컴퓨터에 의해 생성된다. 고유한 단계별 지침을 따르지 않고 솔루션이 제안된다. 때문에 생성된 해는 터무니 없을 수 있다.
(2): 검증 단계에서 결정론적 알고리즘은 입력 인스턴스 I와 무작위로 생성된 해 S를 모두 입력으로 사용하고 무작위 해 S가 올바른 솔루션이면 'yes'를 반환하고 아니면 'no'를 반환한다.
Ex. Traveling Salesperson Problem
외판원 문제를 예시로 들어 이해해보자. 외판원이 n개의 도시를 포함하는 출장을 계획하고 있다고 하자. 각 도시는 도로로 다른 도시와 연결되어 있는데 이동 시간을 최소화하기 위해 영업 사원의 고향 도시에서 시작하여 모든 도시를 한 번씩 방문하고 고향 도시에서 끝나는 최단 경로를 결정하고자 한다. 여기서 tour를 '고향 도시에서 시작하여 모든 도시를 한 번씩 방문하고 고향 도시에서 끝나는 경로'라고 지칭하자.

컴퓨터가 무작위로 tour 목록을 생성한다고 가정하자. 여기서 우리는 '각 tour 목록의 총 가중치가 15이하인 투어를 나타내는가' 라는 결정 문제를 설정할 수 있다. 간단히 수도 코드로 표현해보자.
bool isValidTour (tour)
{
if(the number of vertices in the list is n+1
&& the first n vertices are distinct
&& the first and the last vertices are identical?)
return True;
else
return False;
}
bool verify(WeightedDirectedGraph G, int d, String tour){
if ( isValidTour (tour) && length of all edges in tour <= d)
return true
else
return false
}isValidTour()는 주어진 tour가 유효한지 판단하는 함수이고,verify()는 외판원 문제에서 주어진 tour가 유효하고 가중치 합이 d보다 적은지 판단하는 함수이다. 이처럼 검증 알고리즘이 다항 시간 알고리즘인 경우 해당 알고리즘은 다항 시간 비결정적 알고리즘이라고 한다.
Definition of P and NP Classes
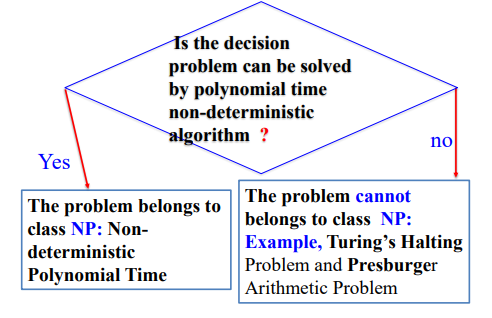
- 클래스 P: 결정론적 다항 시간 알고리즘으로 해결할 수 있는 모든 결정 문제의 집합
- 클래스 NP: 다항 시간 비결정적 알고리즘으로 해결할 수 있는 모든 결정 문제의 집합
- 다항 시간 검증성은 class NP에 속하는 문제의 속성
- 검증 단계에서는 해인 난수 문자열을 생성하는데 필요한 시간을 고려하지 않음
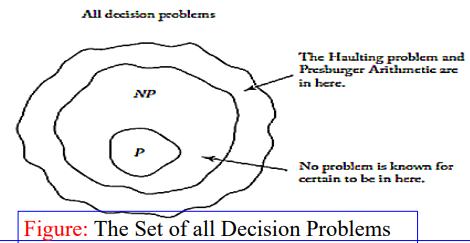
fig 6는 모든 결정 문제의 집합을 보여준다. 이 그림에서 NP는 P를 포함하고 있다. 하지만 이는 NP의 문제가 P에 있을 수 없다는 것을 아무도 증명하지 못했기 때문에 사실이 아닐 수 있다. 이는 NP와 P가 동일할 수 있음을 의미한다.
\(P\neq NP\)임을 보이려면 P에 없는 문제를 NP에서 최소한 하나 찾아야 한다. \(P=NP\)임을 보이려면 NP의 각 문제에 대해 적어도 하나의 다항 시간 알고리즘을 개발해야 한다. 이처럼 P와 NP가 같은지에 대한 질문은 컴퓨터 과학에서 중요한 질문이다. 만약 \(P=NP\)라면 대부분의 알려진 결정 문제에 대해 다항 시간 알고리즘이 사용되기 때문이다. 이것은 아직 열려있는 문제이다. 클래스 NP의 문제가 클래스 P에 속하면 클래스 NP의 나머지 모든 문제는 클래스 P에 속한다. 이러한 유형의 문제를 NP-complete 문제(NP 완전 문제)라고 한다.
The Base of Theory of NP-completeness
CNF-Satisfiability Problem
CNF-Satisfiability Problem(충족 가능성 문제)는 1971년에 발견된 최초의 NP 완전 문제이다. 이 문제에서는 부울 표현식을 다룬다. 부울 표현식에는 4가지 개념이 있다.
- 논리(부울) 변수에는 true 또는 false의 두 가지 가능한 값이 있다.
- 리터럴은 논리 변수 또는 논리 변수의 부정이다.
- 절(clause)은 논리적 "or"(v) 연산자로 구분된 일련의 리터럴이다.
- CNF(Conjunctive Normal Form)의 논리적 표현은 논리적 "and"(\(\wedge\)) 연산자에 의한 절의 시퀀스이다. fig 7은 CNF의 논리식이다.

CNF-충족 가능성 결정 문제는 'CNF에서 주어진 논리적 표현의 논리적 변수에 참과 거짓 값을 할당하여 전체 표현을 참으로 만드는 것이 가능한가?'이다.
위의 2개의 instance를 보면 instance 1의 경우 \(x_1=ture, x_2=ture, x_3=false\)를 할당했을 때 전체 표현을 참으로 만들 수 있기 때문에 CNF-충족 가능성 문제에 대한 해답은 yes이다. instance 2의 경우 CNF 만족도에 대한 답은 no이다.
문제를 한번 분석해보자. CNF-충족 가능성 문제는 클래스 NP에 속한다. 그 이유는 첫째, 아무도 이 문제에 대한 다항 시간 알고리즘을 찾지 못했고, 아무도 미래에 다항 시간에 풀 수 없다는 것을 증명하지 못했기 때문이다. 둘째, CNF의 논리 표현식과 변수에 할당된 부울 값 집합을 입력으로 사용하고 전체 표현식이 해당 특정 할당에 대해 참인지 여부를 나타내는 다항 시간 알고리즘을 작성하는 것은 간단하다. 따라서 이 문제가 클래스 P인지에 대한 여부는 알 수 없다.
Transformation Algorithm
우리는 결정 문제 A를 풀고 싶어하고 결정 문제 B를 해결하는 알고리즘이 있다고 하고 문제 A의 모든 인스턴스 x에서 문제 B의 인스턴스 y를 생성하는 알고리즘이 있다고 가정하자. 이러한 유형의 알고리즘을 변환 알고리즘이라고 하며 타음과 같이 표현된다. \(y_1, y_2, ..., y_n = tran(x_1, x_2, ..., x_n)\). 변환 알고리즘과 문제 B의 알고리즘을 결합하면 아래와 같은 문제 A의 알고리즘이 나온다. 문제 A에 대한 알고리즘은 B의 알고리즘도 다항 시간이라면 다항 시간 알고리즘이 될 수 있다.

A의 특정 인스턴스를 B(AB)의 특정 인스턴스로 변환하는 다항 시간 알고리즘이 다음과 같은 경우 결정 문제 A는 결정 문제 B로 다대일(many-to-one)로 축소 가능한 다항 시간이라고 한다.

- 알고리즘은 A의 모든 YES 인스턴스를 B(\(I_A \Rightarrow I_B\))의 YES 인스턴스로 변환한다.
- 알고리즘은 A의 모든 NO 인스턴스를 B(\(I_A \Rightarrow I_B\))의 NO 인스턴스로 변환한다.
그리고 다음과 같은 경우 결정 문제 B를 NP 완전 문제라고 한다.
- class NP에 속함
- 클래스 NP의 다른 모든 문제는 문제 B로 다항 시간으로 환원될 수 있다.
- 쿡 정리: CNF-충족 가능성 문제는 NP-complete. 이 정리는 1971년에 증명되었다. 모든 NP 문제의 공통 속성을 사용함으로써 증명은 모든 NP 문제가 CNF-만족도 문제로 변환되어야 함을 보여준다. CNF 충족 가능성 문제가 클래스 P에 있음을 보여줄 수 있다면 'P = NP'이다.
Definition of NP-complete Problem
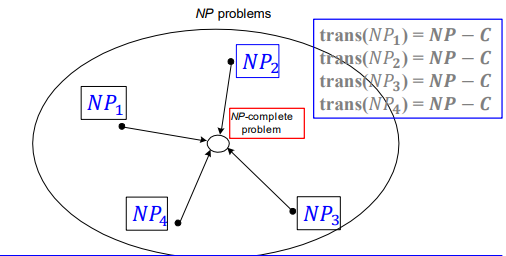
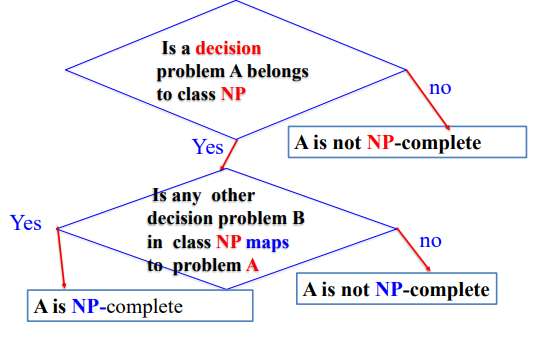
fig 10은 모든 NP 문제를 NP 완전 문제로 다항 시간으로 단축한 것을 나타낸 것이다. NP 문제의 판별법은 fig 11과 같다.
The State of Complexity classes: P, NP and NP-complete
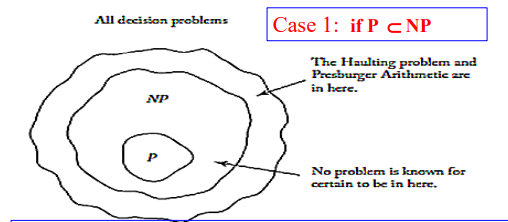
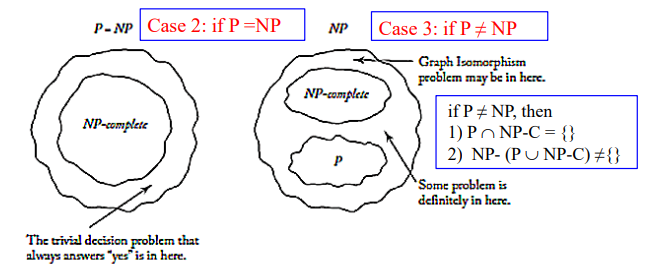
P, NP, NP-complete 3가지 복잡도 클래스의 가능한 관계들에 대해알아보자.
첫번째로는 P가 NP의 부분집합일 때이다. 모든 결정 문제 내부에 NP가 있는데 아직까지 NP이면서 P가 아닌 문제들은 알려지지 않았다.
두번째로는 P=NP일 때이다. P=NP 내부에 NP-complete가 속하는데, P=NP이면서 NP-complete가 아닌 문제로는 항상 yes를 반환하는 (사소한) 결정 문제처럼 다항 시간 알고리즘이 있는 문제이다. 세번째로는 \(P\neq NP\)인 경우이다.
Summary of P, NP and NP-complete
P에 없는 문제가 NP에 있다는 것은 증명되지 않았다. 때문에 NP-P는 비어있을 수 있다. 'P=NP인가?'는 컴퓨터 과학에서 가장 중요한 질문 중 하나이다. \(P \neq NP\)를 보이려면 P에 없는 문제를 NP에서 찾아야하고 \(P=NP\)를 보이려면 NP의 각 문제에 대한 다항 시간 알고리즘을 찾아야한다.
NP-hard and NP-easy Problems
우리는 계속해서 결정 문제에 대해서만 알아봤다. 이 토픽에서는 최적화 문제를 포함한 일반적인 문제를 고려하고 NP-completeness 개념을 비결정 문제로 확장해 볼 것이다.
모든 유형의 문제 B는 NP 문제 A에 대해 'Tran(A)=B'인 경우 NP-hard라고 한다. 이는 NP의 모든 문제가 NP-hard 문제(결정 문제에서 비결정 문제)로 축소됨을 의미한다. 따라서 모든 NP 완전 문제에 해당하는 최적화 문제는 NP-hard이다. 예를 들어 0-1 배낭 문제는 0-1 최적화 문제로 변환될 수 있다.
NP의 일부 B에 대해 'Tran(A) = B'인 경우 일반적인 문제 A를 NP-easy라고 한다. 이것은 모든 문제가 NP 완전 문제로 축소되면 모든 문제가 NP-easy임을 의미한다.
Approximate vs. Exact Algorithms
NP 문제는 문제의 입력 크기에 따라 출력이 기하급수적으로 빠르게 증가하는 요소를 찾아야한다. 예를 들어 주어진 그래프에서 해밀턴 경로 찾기 문제에서 입력은 n개의 정점일 떄 가능한 출력의 수는 n!이다. 그리고 배낭 문제에서 품목의 수가 n개라면, 가능한 출력 수는 \(2^n-1\)개 였다. 역추적/분기 한정 알고리즘은 조합 NP 문제의 소수 인스턴스에 대해서만 정확한 솔루션을 효율적을 제공할 수 있다. 따라서 조합 NP 문제의 모든 경우를 효율적으로 해결하기 위해 근사 알고리즘을 사용할 수 있다.
정확한 솔루션을 생성하는 다항 시간 알고리즘이 없음에도 NP-hard 문제를 구현하는 방법은 주어진 문제의 모든 인스턴스를 해결하고 정확한 해를 얻는 것이 아니라 근사 해를 생성하는 빠른 근사 알고리즘을 사용하는 것이다.
배낭 문제를 탐욕 알고리즘으로 해결하는 것을 예시를 들어보자. 우리는 이 문제에 대한 몇가지 탐욕적인 접근을 생각해 볼 수 있다. 하나는 무게의 내림차순으로 항목을 선택하는 것인데 이것은 더 무거운 품목이 가장 가치있지 않을 수 있다. 또한 가치가 높은 순으로 항목을 선택하는 경우 용량이 효율적으로 사용된다는 보장이 없다. 무게와 가격을 모두 고려한 탐욕적인 전략을 찾을 수 있을까? 이미 우리는 가격/무게 비율을 이용하여 이것이 가능하다는 것을 알았다.
자료 출처
- Introduction to The Design and Analysis of Algorithms / Ananu Levitin
- FOUNDATIONS OF ALGORITHMS / RICHARD E. NEAPORITAN
'알고리즘 > 수업 복습' 카테고리의 다른 글
| More Computational Complexity theory of a problem :The searching Algorithm (0) | 2021.12.21 |
|---|---|
| Introduction to Computational Complexity theory of a Problem: The sorting Algorithm Problem (0) | 2021.12.13 |
| Branch and Bound Method (분기 한정법) (0) | 2021.11.30 |
| Backtracking Algorithm Design Method (백트래킹 알고리즘) (1) | 2021.11.22 |
| Greedy Algorithm Design Pattern 2(탐욕 알고리즘) (0) | 2021.11.08 |




댓글