이전 게시글에 이어서 Greedy Algorithm(탐욕 알고리즘, GA)의 또 하나의 예시인 허프만 이진 코드 트리(Huffman Binary Code Tree)에 대해 알아보자. 그리고 헷갈릴 수 있는 Dynamic programming(DP)과 GA의 차이점에 대해서도 살펴보자.

Huffman Binary Code Tree

해당 알고리즘은 데이터 파일(텍스트, 오디오, 이미지 등)을 효율적으로 인코딩할 때 사용된다. 즉 최대한 압축률을 크게 하는 것이 목적이다. 우선 파일을 어떤 방식으로 나타내는지 부터 알아야겠다. 파일을 나타내는 일반적인 방법은 이진 코드(bit)를 사용하는 것이며 문자는 고유한 코드 워드(이진 문자열)로 표시된다.

Type of Binary Code

여기서 이진 코드의 유형을 두가지로 나눠볼 수 있다. 고정 길이 이진 코드(fixed-length binary code): 각 문자는 동일한 비트 수로 표시된다. 예를 들어 문자 집합이 {a, b, c}인 경우에는 각 문자를 코딩하는데는 2 bit가 필요할 것이다. 'a: 00, b: 01, c: 11' 처럼 표현할 수 있으니 말이다. 만약 파일 내용이 'ababcb'라면 인코딩될 때 2*6=12bit로 인코딩된다. 그렇다면 문자 집합 내부의 문자의 개수가 n개라면, 문자 하나를 표현하기 위해서는 \(log_{2}n\)(n은 짝수)나 \(log_{2}(n+1)\)(n은 홀수)개의 bit가 필요하다. 당연히 표현할 문자가 다양하다면 비효율적이다.

fig 1은 고정 길이 이진 코드의 예시인 아스키 코드(ASCII)이다. 다음과 같이 문자하나를 표현하는데 고정된 길이의 비트 문자열을 사용한다.

다른 유형은 가변 길이 이진 코드(variable-length binary code)이다. 다른 문자는 다른 비트 수로 표시될 수 있다. 예를 들어 문자 집합이 {a, b, c}인 경우 각 문자를 'a: 10, b; 0, c: 11'로 표현할 수 있다. 해당 코드 워드를 적용하면 'ababcb'라는 파일 내용을 인코딩하는데는 2*3+1*3=9bit로 인코딩 된다. 이렇듯 가변 길이 이진 코드는 고정 길이 이진 코드보다 효율적이다. 때문에 최적 이진 코드라고 할 수 있다.

우리는 주어진 파일의 문자들에 대한 최적 이진 코드를 알아내는 알고리즘을 구하는 것이 목적이다. 이는 파일을 최소 비트 수로 나타낼 수 있게 한다. 개념을 정리하자면 이진 코딩 알고리즘(binary coding algorithm)은 주어진 파일의 알파벳 문자 수에 비트 문자열을 할당하는 것이다. 그리고 코드 워드(code word)는 파일의 문자에 할당되는 비트 문자열이다.

How to read Bit Stream?

가변 길이 이진 코드를 이용하여 파일이 인코딩되면 비트 스트림이 저장될 것이다. 이를 디코딩 할 때, 고정 길이인 경우에는 정해진 길이에 맞춰서 문자들을 구분할 수 있는데 가변 길이인 경우에는 어떻게 문자들을 구분할까? 바로 접두부 코드(prefix-free binary code)를 사용하면 된다. 접두부 코드라는건 한 문자의 코드 워드는 다른 문자 코드 워드의 접두사가 될 수 없다는 것이다. 예를 들어 '01'이 'a'에 대한 코드 워드라면 '011'은 'b'에 대한 코드워드가 될 수 없다. 접두부 코드는 파일의 문자를 말단(리프) 노드로 하는 이진 트리 자료 구조로 나타낼 수 있다.

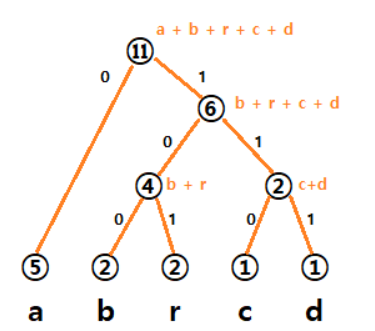
만약 문자 집합이 {a, b, r, c, d}라면 다음과 같은 이진 코드 트리가 만들어 질 수 있다.

일단 이진 코드 트리가 만들어졌다고 하고 디코딩 과정을 살펴보자면, 우선 파일의 첫 번째 비트에서 시작하여 이진 코드 트리를 검색한다. 그런 다음, 각각 0또는 1이 발생하는지 여부에 따라 왼쪽/오른쪽 아래로 이동하는 비트 시퀀스를 따른다. 그리고 단말 노드에 도달하면 문자를 얻을 수 있다. 그리고 다시 트리의 루트로 돌아가서 다음 비트부터 해당 절차를 반복한다. 예를 들어 '1->0->1'순으로 루트에서 아래로 이동하면 'r'을 얻을 수 있는 것이다.

우리는 만들 수 있는 이진 코드 트리 중에 최적 이진 코드 트리를 찾아야한다. 이를 위해서는 당연히 파일내 더 많은 수의 문자에 더 짧은 코드 워드를 할당하고 적은 수의 문자에 더 긴 코드 워드를 할당해야 할 것이다. 위에서 말했듯이 말단 노드가 주어진 알파벳을 나타내는 이진 트리 자료 구조를 사용한다. 모든 왼쪽 간선에는 '0'을 써주고 오른쪽 간선에는 '1'을 써준다. 각 알파벳(말단 노드)의 코드 워드는 트리의 루트에서 해당 단말 노드까지의 간선의 값의 시퀀스이다.

Huffman Binary Coding Algorithm

허프만 코드 트리는 최적 코드라고 하는 최적의 prefix-free binary code를 생성한다. 파일에서 n개의 문자를 인코딩하는 허프만 알고리즘의 단계를 간략히 살펴보자면,

단계(초기화 단계): 하나의 노드로 구성되는 n개의 트리들을 구성한다. 각 트리의 루트에는 각 문자의 빈도를 기록한다.
fig 3
단계: 하나의 큰 트리가 얻어질 때까지 다음 단계를 n -1번 반복한다. 즉 한번 반복에 두개의 트리가 합쳐지는 것.
- 가중치가 가장 작은 두 개의 이진 트리를 하나로 결합하여 결합된 트리의 가중치를 두 트리 가중치의 합과 같게 만든다.
- 왼쪽 간선을 '1'로 표시하고 오른쪽 간선을 '0'으로 표시한다.
  
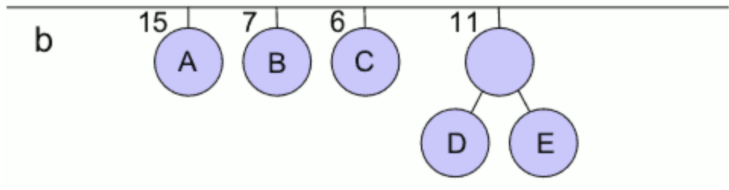
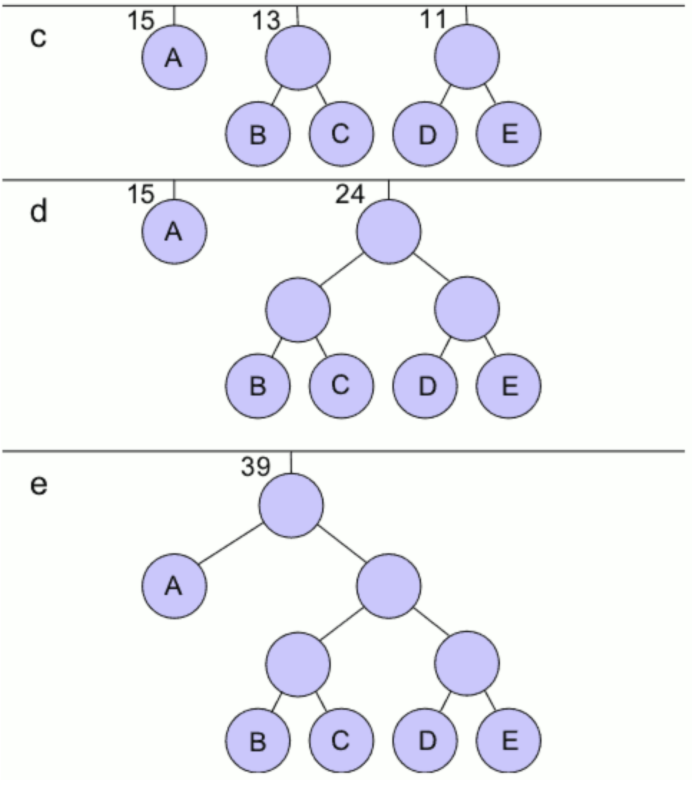
  fig 4

※ 허프만 알고리즘은 MST의 크루스칼 알고리즘과 유사

※ 여기서의 이진트리는 값이 같을 때를 제외하고 오른쪽 자식이 왼쪽 자식보다 큰 값을 가진다.

Pseudo code of Huffman Algorithm

우선 다음과 위에서 사용한 노드는 다음과 같은 구조체로 표현할 수 있다.

struct nodeType
{
    char symbol; //value of character
    int freq; // frequency of character in a file
    nodeType* left; // pointer to left node
    nodeType* right; // pointer to right node
}

이를 이용하여 코드를 표현하면 fig 5와 같다.

노드들(이진트리)은 최소 우선순위 큐(PQ)라는 자료구조에 담긴다. n을 파일의 고유 문자 수라고 하면, 처음에는 n개의 이진트리가 있도록 초기화 한다. PQ를 pop하면 frequency가 가장 작은 node가 pop된다. n-1번의 반복에서 한 노드를 새로 생성하고 오른쪽과 왼쪽 간선에 frequency가 가장 적은 이진 트리 2개를 연결하고 이 들의 frequency 합을 새 노드의 frequency 값으로 한다.

Example

예시로 이해해보자. fig 6처럼 5개의 문자와 각 문자에 대한 빈도가 주어져 있다. 이를 사용하여 허프만 트리를 만들어보자.

우선 병합 작업전에 각 반복에서 빈도(frequency)에 대해 오름차순으로 정렬해야 한다. 그래야 fig 7처럼 앞의 2개를 뽑아 병합할 수 있기 때문이다. fig 6에서는 이때 PQ를 사용했었다. 그러면 각 반복마다 2개의 이진 트리들이 병합된다.

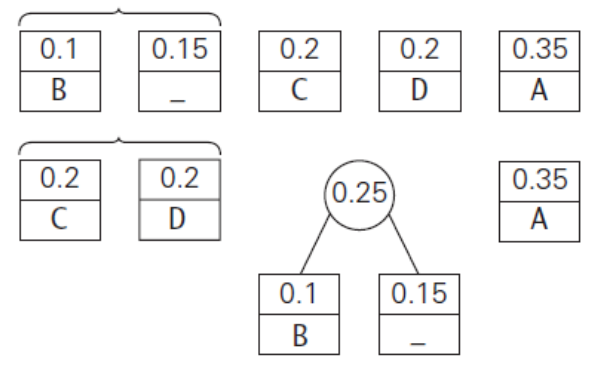
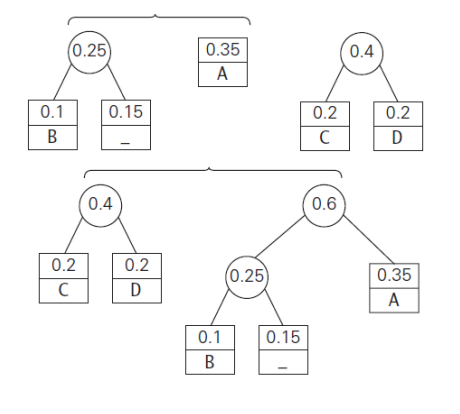
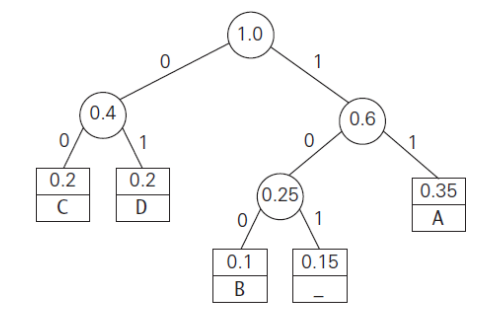
n-1번의 반복이 이뤄지면 fig 6.3과 같은 허프만 트리를 얻을 수 있다. 이를 토대로 각 문자들이 어떻게 인코딩되는지 표로 정리해보면 fig 6.4와 같다.

Compression efficiency(reduction of bits)

그렇다면 허프만 알고리즘을 사용하여 인코딩하면 고정 길이 이진 코드를 사용할 때보다 얼마나 더 효율적일까? 위의 Example을 예시로 살펴보자.

위의 예시에서 얻어진 5개의 문자들의 평균 코드 워드길이는 각 문자의 (frequency)*(cordword의 비트수)를 모두 더한 값인 2.25이다. 그리고 고정 길이 이진 코드를 사용했다면 각 문자들은 3-bit로 이루어질 것이다.

그러므로 압축효율은 \((\frac{b_{f}-b_{v}}{b_{f}})*100=(\frac{3-2.25}{3})*100=25\)%로 표현할 수 있다.

Summary: Dynamic Programming & Greedy Algorithm

이제 동적 프로그래밍과 탐욕 알고리즘의 차이점을 다시 한번 정리하면서 탐욕 알고리즘을 마무리해보자.

어떤 (최적 조건을 만족하는)최적 문제가 주어졌을 때, 두 방법을 이용하여 해결할 수 있다. 각 기법을 이용하여 해결했던 문제들을 살펴보자.

Problem 1: Shortest paths from many sources to many destinations

여러 시작점에서 여러 도착점까지의 최단 경로 문제는 Floyd algorithm같은 동적 프로그래밍 알고리즘을 사용하여 계산했었다. 시간 복잡도는 \(\theta(n^3)\)였었다.

Problem 2: Shortest paths from one source to many

하나의 시작점에서 여러 도착점까지의 최단 경로 문제는 Dijkstra Algorithm을 이용하여 해결할 수 있었다. 시간 복잡도는 \(\theta(n^2)\)였었다. 이 문제(problem 1에 포함)는 물론 동적 알고리즘으로도 해결할 수 있으나 \(\theta(n^3)\)라는 매우 긴 시간 복잡도를 가지고 더 빠르게 수정할 방법이 없다.

Problem 3: The zero-one Knapsack

이 문제는 배낭을 메고 있는 도둑이 보석 가게에 침입하여 물건을 훔치려 할 때, 가방의 용량을 초과하지 않으면서 훔친 물건들의 총 가격을 최대화하려는 것이다.

S = {i1, i2, ..., ii, ..., in}은 물건들의 집합
w = {w1, w2, ..., wi, ..., wn}은 각 물건들의 무게
p = {p1, p2, ..., pi, ..., pn}은 각 물건들의 가격
\(W_{max}\)는 배낭의 최대 용량
Z는 S의 하위 집합

다음과 같이 상황을 정의했을 때, 문제는 Z에 담기는 물건들의 무게 총합이 \(W_{max}\)보다 적으면서 가격합이 최대인 경우의 Z를 구하는 것이다.

Trial and Error Solution

집합 S에는 \(2^n\)개의 부분 집합이 있으므로 가능한 각 부분 집합을 확인하고 최적의 부분 집합을 선택할 수 있다. 하지만 이러한 방법은 기하급수적인 시간 복잡도를 갖게 된다.

Greedy Algorithm Solution

우선 'p1=10, p2=9, p3=9', 'w1=25, w2=10, w3=10', \(W_{max}=30\)이라고 하자.

기준을 정해야하는데 가격이 높은 물건을 우선으로 선택하는 경우부터 살펴보자. 이때는 아이템들을 가격에 대해 내림차순으로 정렬한뒤 가장 앞의 물건을 선택할 수 있을 것이다. 지금 같은 경우에는 i1이 선택되는데 이렇게 되면 공간이 5밖에 남지 않으므로 5라는 공간이 낭비되고 이 경우가 최적 해도 아니다.

그럼 기준을 바꿔서 무게당 가격(가격/무게)이 큰 것부터 선택하는 경우를 살펴보자. 'p1/w1=0.4, p2/w2=0.9, p3/w3=0.9'라는 결과를 얻을 수 있다. 때문에 i2, i3를 선택할 수 있는데, 최대 용량을 초과하지도 않고 이전에 세운 기준일 때보다 더 많은 값을 얻을 수 있다. 때문에 해당 인스턴스에서는 두번째 기준이 더 나은 결과를 도출한다.

하지만 인스턴스에 따라 첫번째 기준이 더 좋은 경우가 있을 수 있다. 그러므로 zero-one knapsack문제는 탐욕 알고리즘으로는 완벽히 해결할 수 없다. 만약 물건의 일부분을 떼어갈 수 있다면 이때는 '무게당 가격'을 기준으로 모든 인스턴스에 대한 최적해를 구할 수 있긴 하다.

Dynamic programming Solution

이제 동적 프로그래밍으로 해당 문제를 해결해보자. 그전에 이 문제가 최적의 원칙을 만족하는 가를 따져보자. 최적해에서 Z의 원소 개수가 n개라고 하자. 만약 in을 포함하지 않으면 Z는 i1,...,i(n-1)을 포함하는 최적 부분집합이다. 그리고 Z에 in이 포함되어 이다면 Z에 있는 물건의 총 가격은 'in의 가격+첫번째 물건으로 i(n-1)을 선택할 때 얻은 최적 이익'과 같으므로 Z의 총무게 \(w_t\)는 \(W_{max}-w_n\)보다 클 수 없다. 때문에 최적의 원칙을 만족하고 다음과 같은 반복 관계를 얻을 수 있다.

fig 7.2는 한 인스턴스에 대한 예시이다.

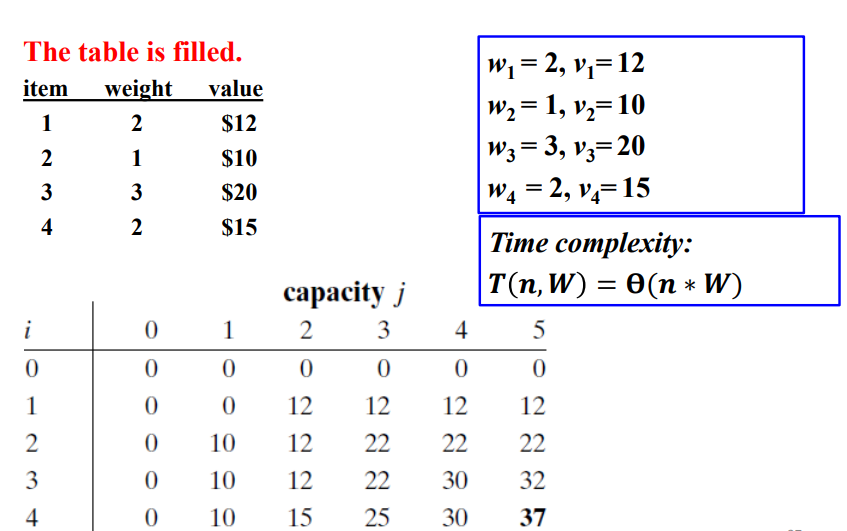
이차원 배열로 이루어진 p가 채워졌다. 이에 소요되는 시간 복잡도는 \(\theta(n*W)\)이다. 그럼 이것을 이용하여 어떤 물건이 가방에 들어갔는지를 알아내야한다. 이를 위해서는 배열을 역방향으로 스캔해야 한다. p[i][w]는 p[i-1][w]와 p[i-1][w-wi]로 계산되기 때문에 우리는 i번째 행에서 물건을 선택한 후에 i-1행에서 물건을 선택할 수 있다. 예시를 보면 p[4,5]>p[3,5]이므로 i4는 Z에 포함되고, p(3,3)=p(2,3)이므로 Z에 포함되지 않는다. 이런식으로 역방향으로 스캔해보면 i1, i2, i4가 가방에 들어가야 하는 것을 알 수 있다. 이때의 시간복잡도 역시 \(\theta(n*W)\)가 소요된다.

그런데 여기서 만약에 \(W_{max}\)가 n에 비해 압도적으로 큰 값을 가진다면 이는 trial&error 알고리즘보다 더 큰 시간 복잡도를 가지게 된다. 이는 배열 p의 모든 항목을 다 채워야하기 때문이다. 그러므로 만약 채워야할 항목들만 계산해주면 위와 같은 시간 복잡도를 개선할 수 있을 것이다.

Improved Dynamic Programming Solution

'\(p_1=50, p_2=60, p_3=140, w_1=5, w_2=10, w_3=20, W_{max}=30\), n=(물건의 개수)'라는 인스턴스를 설정하고 좀더 개선된 해결책을 살펴보자.

우선 위에서는 배열 p[n][W]의 모든 항목을 다 구했지만 여기서는 필요한 항목들만 구함으로써 시간 복잡도를 개선한다. 때문에 우선 어떤 항목들을 필요로 하는지 알아야한다. 위의 방법에서 우리는 p[3][30]부터 거슬러 올라가면서 어떤 물건이 해에 포함되는지 구했다. 그래서 우리는 row 3에서는 p[3][30]의 값을 알아야한다. p[3][30]은 p[3-1][30]&[3-1][\(W-w_3\)]으로부터 구해질 수 있으므로 row 2에서는 두 개의 값을 알아야 한다. 그렇다면 row 1에서는 p[2-1][30]&p[1][\(W-w_2\)]와 p[2-1][10]&p[2-1][\(10-w_2\)], 총 4개의 항목을 구해야한다.

어떤 항목을 구해야할지 알았다면 p[n][W]에서 필수적으로 알아야하는 항목을 재귀를 이용하여 row 1부터 계산한다. 이때 다음과 같은 재귀 관계를 따를 것이다.

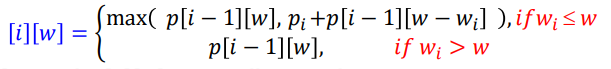
이를 이용하면 p[1][0]=0, p[1][10]=50, p[1][20]=50, p[1][30]=50 / p[2][10]=60, p[2][30]=110 / p[3][30]=200을 구할 수 있다. 기존 방법으로는 90개의 항목을 구해야했지만 이 방법으로는 7개의 항목만 구하면 된다.

물건의 개수가 n개라고 하면 최악의 경우에 row n에서는 2^0개의 항목, row (n-1)에서는 2^1개의 항목, ..., row 1에서는 2^(n-1)개의 항목을 구하면 된다. \(2^0+2^1+...+2^{n-1}=2^n-1\)이므로 worst-case 시간 복잡도는 \(T(n)=\theta(2^n)\)이다. 그런데 \(1\leq i\leq n \)에 대해 \(w_i=1\)이고 \(n=W+1\)이면, \(T(n)=\theta(n*W)\)이므로, 최종 worst-case 시간 복잡도는 \(T(n)=\theta(min(2^n, n*W))\)다.

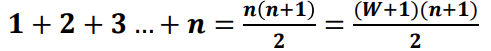
이 같은 방법을 Memory Function이라고 한다. 지금껏, 우리는 재귀 관계에서 하위 문제가 겹치는 경우 두가지 방법을 사용했었다.

recursive solution(직접적인 하향식 접근): 일반적인 하위 문제를 두 번 이상 풀기 때문에 기하급수적인 시간복잡도를 가진다.
dynamic programming(상향식 접근): 모든 작은 하위 문제에 대한 해로 표를 채운다. 각 하위 문제는 한번만 해결되나, 이렇게 얻어낸 해 중 일부는 원래 문제의 해를 구하는데 불필요한 경우가 많다.

따라서, memory function에서는 이 두 가지 접근 방식의 장점을 합친다. 즉 필요한 하위 문제를 한 번만 해결하도록 설계하는 것이 목표이다.

이 방법은 상향식 동적 계획법에서 사용하는 종류의 테이블을 유지함으로써 하향식 방식으로 주어진 문제를 해결한다. 우선 테이블의 모든 항목을 "null" 기호로 초기화하여 지금까지 계산되지 않았음을 나타낸다. 그리고 새 값을 계산할 때마다 이 메서드는 먼저 테이블의 해당 목록을 확인하고 "null"이 아니면 이것을 사용하고 그렇지 않다면 재귀 호출로 계산한 다음 테이블에 기록한다. 이러한 과정을 수도 코드로 나타내면 fig 7.5와 같다.

자료 출처

Introduction to The Design and Analysis of Algorithms / Ananu Levitin
FOUNDATIONS OF ALGORITHMS / RICHARD E. NEAPORITAN
fig 2 / play ground / https://playground10.tistory.com/98
fig 3, 4/ kjh.log / https://velog.io/@junhok82/%ED%97%88%ED%94%84%EB%A7%8C-%EC%BD%94%EB%94%A9Huffman-coding

저작자표시

'알고리즘 > 수업 복습' 카테고리의 다른 글

Branch and Bound Method (분기 한정법) (0)	2021.11.30
Backtracking Algorithm Design Method (백트래킹 알고리즘) (1)	2021.11.22
Greedy Algorithm Design Pattern 1(탐욕 알고리즘) (0)	2021.10.19
Dynamic Programming Design Pattern (동적 계획법) (0)	2021.10.13
Divide and Conquer design pattern(분할정복) (0)	2021.10.04

학습기록

Greedy Algorithm Design Pattern 2(탐욕 알고리즘)