이전에는 알고리즘의 효율성을 판단하는 방법을 살펴봤었다. 이제 처음에 언급했듯이 하나의 디자인 패턴을 이용하여 몇가지 문제를 해결해보고 이를 분석해보자.
Introduction to Divide-and-Conquer
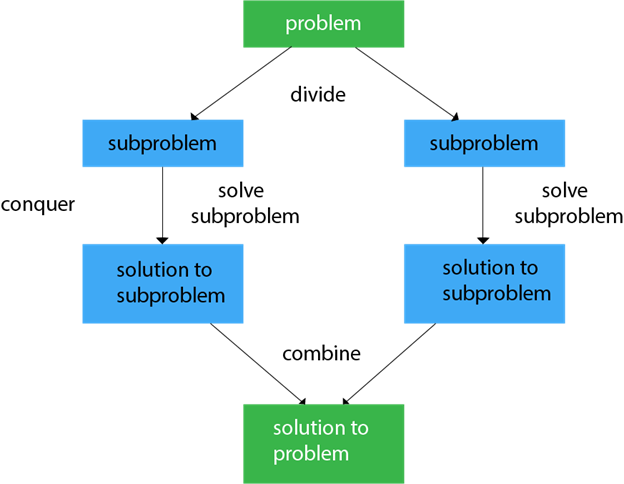
divide&conquer. 한글로 해석하면 나눠서 정복하는 것이다. 즉 input으로 주어진 instance가 너무 거대할 때, 이를 두개 이상의 작은 부분으로 나누어 이것들을 하나씩 해결해나가는 것이다. 작은 부분들을 해결한 결과물을 합치게되면 원래 해결하고자 했던 문제를 해결할 수 있게 되는 것이다.
만약 나눠진 문제가 해결하기에 여전히 큰 문제라면, 이를 해결할 수 있을 때까지 더 작은 조각으로 나눌 수 있다. 이러한 divide&conquer 접근은 original problem의 solution이 밑으로 내려가면서 작은 문제들을 해결하면서 얻어지기에 하향식(top-down)접근이다.
이전 글을 봤다면 재귀 함수(recursive function)을 통해 이러한 접근을 인식할 수 있다는 것을 짐작할 수 있다. 우선 문제 해결 단계에 초점을 맞추어 재귀 관계를 설정하면 이후 시스템이 call stack을 이용하여 solution을 얻기 때문이다. 재귀 알고리즘을 이용하여 문제를 해결할 수 있게되면 이후 iterative version을 작성하여 효율적인 알고리즘을 작성한다. 보통 iterative algorithm이 효율성이 더 좋기 때문이다. 하지만 모든 문제를 iterative version으로 변환할 수 있는 건아니다. 자세한 건 이후에 확인할 수 있을 것이다.
3 steps of Divide&Conquer Argoritm Design
해당 알고리즘 디자인 전략은 3단계의 기본 절차를 밟는다.
- Divide: 문제의 instance를 두 개 이상의 더 작은 instance로 나눈다.
- Conquer(solve): 작아진 문제를 해결한다. 만약 문제가 충분히 작지 않다면 재귀 함수를 이용한다.
- (필요하다면)Combine: 기존 instance의 solution을 얻기위해 작은 문제들의 solution들을 합친다. problem에 따라 필요없을 때도 있다.
이제 몇가지 문제에 해당 알고리즘을 적용해보자.
Binary Search(이진 탐색)
이진 탐색에 해당 디자인 패턴을 적용해보자.
- Problem: 크기 n인 정렬된 배열 S에 k(Key)라는 값이 있는지 판단
- Inputs: 정렬된 배열 S[0, ..., n-1], Key k
- Output: S에서 k와 같은 값이 있는 위치, 만약 k라는 값이 없다면 -1
위의 상황을 토대로 이진탐색을 간단히 알아보자. S = [10, 12, 13, 14, 18, 20]이고 k=18이라고 하자. 우선 배열의 중앙에 위치한 값(13)과 k를 비교한다. k값이 더 크니 이제 이전 중간 위치와 배열 끝의 중간 위치의 값(18)을 k와 비교한다. k값과 동일하니 탐색이 종료된다.
해당 알고리즘은 나눠진 문제의 solution이 기존 문제의 solution과 동일하여 combine 단계가 필요없기에 간단하다.

간단히 표현하면 저러하다. 해당 알고리즘은 인스턴스마다 basic operation 횟수가 다를 수 있으므로 시간복잡도도 달라질 수 있다. worst case 기준으로 알고리즘을 분석해보자. 이전 게시글에 재귀 알고리즘을 분석하는 방법이 설명되어 있다. 문
- input size: 배열에 담기는 item들의 수 n
- Basic operation: k를 S[middle]과 비교
- 시간 복잡도는 worst, best, average가 존재한다.
- worst case 시간 복잡도를 가지는 경우는 k가 배열의 있는 모든 값들보다 큰 상황이다. 그리고 재귀 관계에 따라서, w(n) = w(n/2)+1 (recursive condition), w(1) = 1 (initial condition)이다.
- w(n/2)는 recursive call에서의 비교 횟수이다.
- top level(마지막)에서는 1번의 비교가 필요하다.
- 4에서 얻은 관계식을 n에 대한 함수로 변환한다. W(n) = logn+1
- \(W(n)\in \theta (logn)\)
다음과 같이 iterative version으로 바꿀 수도 있다.

※ Solving Recurrence Relation: Master Theorem
저번 포스팅을 봤으면 알겠지만 재귀 알고리즘은 반복 알고리즘에 비해 시간 복잡도를 구하기 더 어렵다. 우선 관계식을 설정하고 이를 input size n에 대한 함수로 고쳐야하기 때문이다. 그러나 Master Theorem(마스터 정리)를 사용하면 간단하게 이 문제를 해결할 수 있다. 사실 본인은 수식에 매우 약하기 때문에 처음 수식을 봤을 때 매우 당황했다,,,😥 그래도 지금 글을 적으면서 이해해보겠다.
재귀 알고리즘의 관계식은 다음과 같은 형태를 가지는데<
\(T(n)=aT(\frac{n}{b})+f(n), n>1, n=b^k\)
\(T(1)=c\)
where \(f(n)=n^d, a\geq 1, b\geq 2, c\geq0, d\geq 0\)
벌써부터 어지럽다... 일단은 계속 보자. 해당 관계식에서 a, b, f(n)을 이용하여 시간복잡도를 계산하는데 3가지 경우가 있다.
- \(f(n)\in O(n^{\log_{b}a}), T(n)\in\theta(n^{\log_{b}a})\)
- \(f(n)\in \Omega(n^{\log_{b}a}), T(n)\in\theta(f(n))\)
- \(f(n)\in \theta(n^{\log_{b}a}), T(n)\in\theta(f(n)*\log_{}n)\)
조금 전에 봤던 이진 탐색의 예시를 가져오자. w(n) = w(n/2)+1로 관계식이 표현되었다. 위에 정의된 T(n)과 형태가 유사하다!! 모양을 맞춰보면 a=1, b=2, f(n)=1이다. \(\log_{b}a=0\)이므로 3번째 경우를 만족한다(1=1). 그러므로 \(T(n)\in\theta(\log_{}n)\)이다. 정말로 시간복잡도가 구해졌다!!
T(n)을 조금 뜯어보자.우선, n/b가 의미하는 것은 문제가 나눠질 때 생기는 subproblems의 크기이다. 이진 탐색에서는 다음 재귀에서 현재 배열의 절반을 입력으로 받으므로 b=2가 되는 것이다. 그리고 a가 의미하는 것은 b개의 subproblems 중 해결해야하는 subproblems의 갯수이다. fig 2를 보면 알겠지만 함수안에서 자기자신을 '1'번 더 호출한다. 그러면 \(aT(\frac{n}{b})\)가 의미하는 것을 알겠는가? 바로 나눠진 문제를 해결하는데 걸리는 시간이다. 즉 Divide-Conquer-Combine의 3단계에서 Conquer하는데 걸리는 시간이다.
그럼 자연스럽게 \(f(n)\)은 Divide와 Combine에 소요되는 시간인 것이다. 즉 크기 n을 가지는 instance를 b개의 subproblems으로 나누는데 걸리는 시간과 b개의 subproblems을 합치는데 걸리는 시간의 합이다.이진 탐색에서는 combine은 애초에 없고 problem을 나누는데 반복이 사용되지는 않는다. 때문에 f(n)=1이 되는 것이다.
MergeSort Algorithm (병합 정렬)
이번에는 병합 정렬에 대해 알아보고 이를 분석해보자. 병합 정렬은 정렬된 두 개의 다른 배열들을 하나의 정렬된 배열이 되게 합치는 것이다. 보자말자 재귀가 쓰이겠다는 느낌이 팍팍 든다. array가 n개의 요소를 가진다고 가정하고 Divide&Conquer의 3단계를 적용해보자.
- Divide: 기존 array를 n/2 크기를 가지는 subarray 2개로 나눈다.
- Conquer(solve): 각 subarrays를 정렬하여 해결한다. 만약 해결하기에 충분히 적지 않으면 재귀를 이용한다.
- Combine(merge): 두 개의 정렬된 arrays를 하나의 정렬된 array로 합친다.
이를 재귀를 이용하여 pseudo code로 표현하면


다음과 같다. 뭔가 복잡해 보인다. 우선 Mergesort에서 길이 n의 배열 A을 절반으로 쪼개어 각각을 다시 Mergesort 알고리즘에 넣는다. 그리고 이것들을 Merge를 이용해 합치는 것이다.
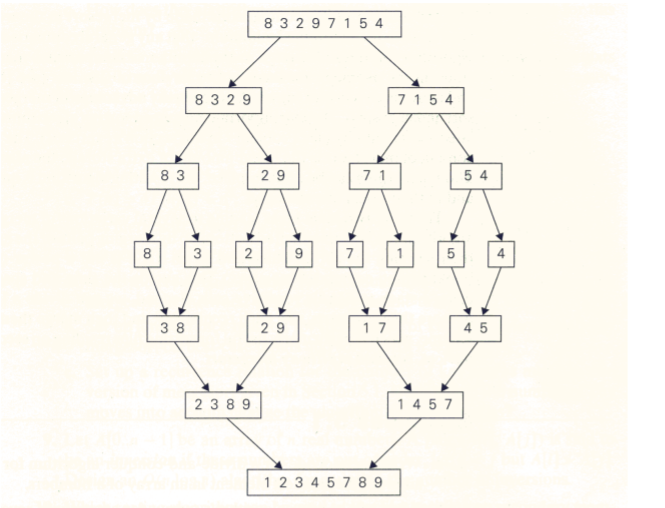
그림으로 병합 정렬 알고리즘의 예시를 표현하면 다음과 같다. 배열을 최대한 작게 쪼갠다음 다시 이것들을 정렬된 배열이 되게끔 합쳐가는 것이다. 이번에도 순서에 맞춰 이것을 분석해보자.
- input size: n(배열의 크기)
- baasic operation: number of key comparisons
- 해당 알고리즘은 every-case time complexity를 가진다.
- 재귀 관계를 정의한다. \(C(n)\)을 key comparison의 횟수라고 하면
- \(C(n)=2C(\frac{n}{2})+C_{merge}(n), n>1, C(1)=0\)
- \(C_{merge}(n)=n-1\), 해당 식은 Divide와 Combine에 관련된 항이다. 배열을 둘로 나누는 것은 constant time이 소요되고 합치는데는 n-1의 시간복잡도를 가진다. 이해가 안되면 fig 4, 5를 참고하자.
- \(C_{w}(n)=2C_{w}(\frac{n}{2})+n-1, n>1\)를 recursive condition, \(C_{w}(1)=0\)을 initial condition이라고 할 수 있다.
- 위에서 마스터 정리를 배웠으니 써먹어보자.
- a=2, b=2, f(n)=n-1이고, \(f(n)=n^{\log_{2}2}\)이니 \(C_{worst}(n)=O(n*\log n)\)
Quick sort
퀵 정렬에 대해서도 살펴볼건데, 이름부터 quick이 들어가는걸로 봐선 앞의 소개한 알고리즘보다 빠르지 않을까라는 생각이 든다. 이름값을 하는지 보도록 하자.
merge sort에서는 배열을 나눌 때, 절반으로 균등하게 나눴었다. 하지만 quick sort에서는 배열을 불균등하게 나눈다. 이전 알고리즘보다 과정이 조금 복잡하니 어떤 과정으로 진행되는지 알아보자.
과정 설명
- 배열 내부에 한 요소를 선택하고 이를 피벗(pivot)이라고 하자.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로, 피벅보다 큰 요소들은 모두 피벗의 오른쪽으로 옮긴다.
- 피벗을 제외하고 왼쪽 배열과 오른쪽 배열을 다시 정렬한다. 이때 분할된 배열들에 대해 재귀를 이용하여 정렬을 반복한다. 이때 피벗은 새롭게 정해야한다.
- 부분 배열들이 더이상 분할이 되지 않을 때(크기가 1이하)까지 이를 반복한다.
Divide&Conqer의 3단계로도 나타내보자
- Divide: 입력 배열을 피벗을 기준으로 비균등한 2개의 부분배열(피벗 왼쪽은 피벗보다 작은 요소들, 오른쪽에는 피벗보다 큰 요소들)로 분할한다.
- Conquer: 부분 배열을 정렬한다. 만약 부분배열의 크기가 충분히 작지 않으면 재귀를 이용해 다시 divide와 conqer을 수행한다.
- Combine: 정렬된 부분 배열들을 하나의 배열로 합친다.
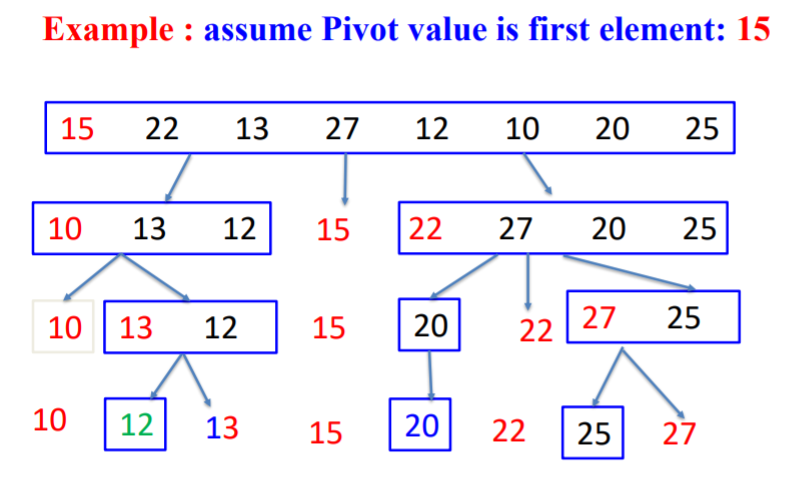
그림으로 나타내면 이런식이다. 여기까지 보면 뭔가 하나 걸리는게 있다. "그럼 pivot은 어떤 기준으로 정해야 하는거지?"다.
Lomuto Partitioning

로무토 파티션은 pivot의 첫번째 요소를 이용한다. 해당 알고리즘의 input은 배열 A[0...n-1]의 부분 배열A[l...r]이다. 그리고 output은 A[l...r]의 분할과 새로운 pivot위치이다. 그림으로 과정을 살펴보자.
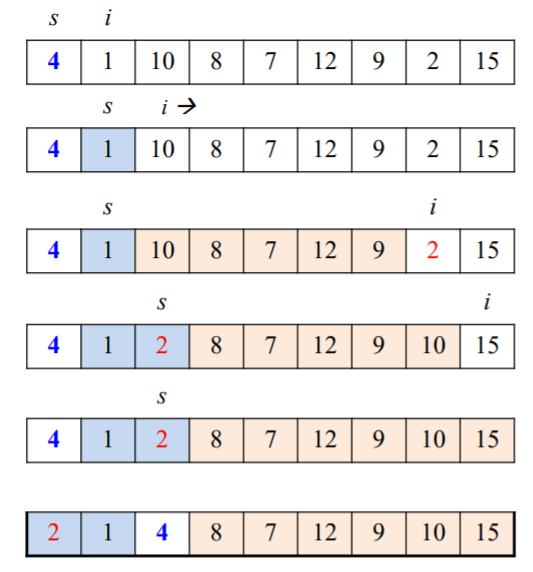
처음에는 s를 첫번째 인덱스 l로, pivot을 A[l]=4로 지정한다. i는 l+1부터 시작해서 r까지 증가한다. 반복하는 중에 A[i]가 pivot보다 작다면 s를 1증가시킨다음 s위치의 요소와 i번째 요소 위치를 바꾼다. 그림에서 1,2번째 줄 사이에서 s와 i는 동시에 2번째 인덱스가 되기에 위치 변경이 이뤄지지 않는다. 그러다가 i가 '2'가 있는 인덱스만큼 증가하면 이때는 s에 1이 더해져서 '10'과 '2'의 위치가 서로 바뀌게 되는것이다. 그리고 마지막에는 A[l]과 A[s]의 위치를 바꿔준다.
이것의 결과는 그림과 같이 pivot 기준으로 왼쪽에는 pivot보다 작은 값이, 오른쪽에는 pivot보다 큰 값이 위치하게 된다. 그리고 처음에 첫번째 인덱스였던 s가 이제는 세번째 인덱스가 되었다.
Hoare's Partitioning
두번째 분할법으로는 호어 파티션을 살펴보자.


로무토와 다른점이 무엇일까? 여기서도 처음에 pivot을 첫번째 인덱스로 둔다. 그리고 i를 두번째 인덱스, j를 마지막 인덱스로 설정한다. 그리고 반복문을 i값은 증가시키고 j값은 감소시키면서 i>=j일 때까지 돌린다. i는 증가하다가 pivot보다 큰값에 위치하면 잠시 멈추고, j는 감소하다가 pivot보다 작은 값을 만나면 멈춘다. 그러다가 i, j가 둘다 멈추게 되면 이때 i와 j위치의 값을 서로 바꿔주고 다시 증가, 감소를 진행한다. 이런 과정을 반복하다가 i>=j가 되면 pivot과 j에 위치한 값들을 서로 바꿔주게 된다. 이렇게 되면 여기서도 pivot기준 왼쪽은 pivot보다 작은 값이, 오른쪽은 pivot보다 큰 값이 위치하게 된다.
Pseudo code of Quicksort

최종적으로 fig 11과 같은 quick sort 알고리즘을 얻을 수 있다.
The Complexity of Quicksort
그럼 퀵 정렬의 시간복잡도도 알아봐야하지 않을까? 앞에서 봤듯이 과정이 이전 다른 알고리즘보다 복잡하다는 생각이 들었다. 퀵 정렬 시간복잡도를 부분부분 이해해보자.
우선 C(n)을 배열을 정렬하기 위한 숫자 비교 횟수(conquer), f(n)을 나누는데(divide) 걸리는 시간이라고 하자. 위에서 봐서 알겠지만 정렬된 요소들은 각 제자리에 위치하기 때문에 combine은 필요없다.
- case 1: 위의 예시를 예로 들면 i,j가 교차할 때는 f(n) = n + 1
- case 2: i, j가 일치할 때 f(n) = n
그리고 해당 알고리즘은 instance에 따라 시간복잡도가 달라질 수 있으므로 every-case를 가지지 않는다.
- best case: 느낌적으로도 알 수 있듯이 파티션으로 pivot의 위치가 결정될 때 이것이 배열의 중앙이라면 같은 크기의 부분배열 2개로 나눠지므로 가장 작은 시간복잡도로 나눠진다. 마스터 정리를 이용해 시간복잡도를 구해보면
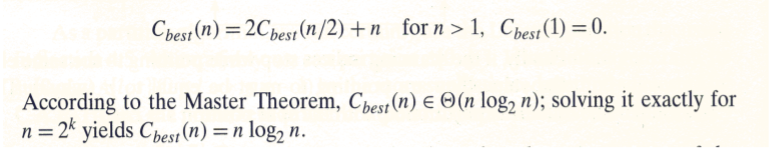
- worst case: best case와 반대되는 경우를 생각해보자. pivot이 한쪽으로 쏠릴수록 더 큰 시간 복잡도를 가지게 된다. 그러므로 이미 정렬이 된 배열에 퀵 정렬을 사용하게 되면 pivot은 한쪽 끝에 위치하게 된다. 한 부분배열이 n-1개의 요소를 가진다. 즉 Divide 한번에 사이즈는 1감소한다. 즉 첫번째 재귀에서는 (n+1)번의 비교, 두번째 재귀에서는 n번의 비교, .... 가 필요하다.
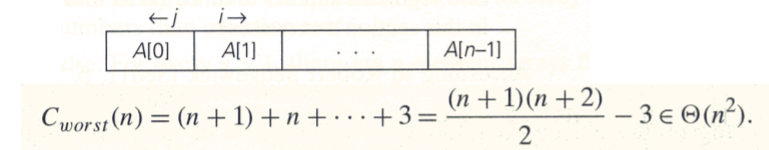
자료출처
- fig 1 / DW dev blog / http://dawoonjeong.com/algorithm-divide-conquer/
- fig 2 / Design / https://designatedroom87.tistory.com/5
- fig 4 / 코딩팩토리 / https://coding-factory.tistory.com/136
- Introduction to The Design and Analysis of Algorithms / Ananu Levitin
- FOUNDATIONS OF ALGORITHMS / RICHARD E. NEAPORITAN
'알고리즘 > 수업 복습' 카테고리의 다른 글
| Greedy Algorithm Design Pattern 2(탐욕 알고리즘) (0) | 2021.11.08 |
|---|---|
| Greedy Algorithm Design Pattern 1(탐욕 알고리즘) (0) | 2021.10.19 |
| Dynamic Programming Design Pattern (동적 계획법) (0) | 2021.10.13 |
| Algorithm Efficiency(알고리즘 효율성) (0) | 2021.09.18 |
| Introduction: 알고리즘에 대해 (0) | 2021.09.06 |




댓글