이번에 알아볼 디자인 패터은 탐욕 알고리즘(GA, Greedy Algorithm)이다. 해당 디자인 패턴은 저번에 알아본 동적 계획법과 마찬가지로 최적화문제(max/min)를 해결하는데 쓰인다. 즉 문제가 최적 부분 구조를 가지고 있어야 한다고 했었다. 이에 대해 다시 짚고 넘어가자면 origin program의 최적해(solution)가 부분 문제의 최적해들로써 구성되어야, 그 문제가 최적 부분 구조를 가졌다고 할 수 있는 것이다. 이전 글의 예시들을 다시 본다면 이해할 수 있을 것이다.
계속하자면, GA의 설계 전략은 최적해를 얻을 때까지 일련의 절차를 따르는데, 이때 현재 단계의 action에 따른 일련의 과거/미래 단계의 action의 잠재적 단점은 고려하지 않는다(\(A_{1} \rightarrow A_{2} \rightarrow ... A_{c} \rightarrow A_{c+1} \rightarrow A_{c+2} \rightarrow ... A_{n}\)). 현재 단계에서, 이 전략은 데이터 항목을 순서대로 가져오려고 시도하며, 이전에 했거나 미래에 할 선택에 관계 없이 몇몇 부분(local)의 기준이나 제약조건에 따라 최선의 것으로 보이는 항목을 취한다.
GA은 일련의 선택을 함으로써 해(solution)에 도달하며, 각각의 선택은 현재 단계에 가장 좋아 보이는 것을 택한다. 따라서 각 선택은 해당 부분의 최적해를 제공하며 이는 다른 선택에 미치는 잠재적 위험을 고려하지 않기에, global한 최적해를 제공할 수도, 그렇지 않을 수도 있다(최적해 보장X). 역시 일반화된 내용으로 들으면 너무 추상적인 것 같다. 예시를 확인해보자.
Ex1. Coin Change for a Purchase
이 문제는 \(d_1 < d_2 < ... < d_m\)값들을 가지는 동전이 무제한으로 주어졌을 때, 특정 금액 n에 대한 거스름돈을 최대한 동전의 개수가 적게끔 구매자에게 주는 것이다.
첫번째 input instance는 \(d_1=1, d_2=5, d_3=10, d_4=25\), n=48이라고 하자. 이 경우에 GA으로 최적해를 얻을 수 있을까? 각 단계에서의 최적의 선택은 가능하다면 최대한 큰 금액의 동전을 먼저 선택하는 것이다. 즉 동전을 선택하는 기준(순서)은 \(d_4 \rightarrow d_3 \rightarrow d_2 \rightarrow d_1\)이다. \(1d_4+1d_3+3d_1=48\)이고, 동일한 답을 동적 계획법을 통해서도 얻을 수 있으므로 정답은 Yes이다.
두번째 input instance는 \(d_1=1, d_2=10, d_3=25\), n=30이라고 하자. 이 경우에는 탐욕 알고리즘으로 최적해를 얻을 수 있을까? 이 역시 GA에서는 해당 단계에서 가능한 가장 큰 금액의 동적을 택하는 것을 기준으로 설정할 수 있다. 그렇게 되면 \(1d_3+5d_1=30\)이다. 이는 동적 계획법을 사용했을 때와 같은 값을 가지지 않는다. 만약 동적 계획법으로 해를 구했다면 \(3d_3=30\)이 나왔을 것이다. 때문에 해당 instance에서 GA를 사용했을 때는, 부분문제의 최적해를 이용하여 원래 문제의 최적해를 구하지 못했다.
Pseudo Code of GA

fig 1은 위의 문제를 greedy algorithm으로 해결할 때의 수도 코드이다. 이를 살펴보면 GA에서는 과거의 동작을 다시 고려할 수 없다. 일단 어떤 동전이 받아들여진다면, 이는 영구히 해의 일부가 된다. 반대로 거부된다면, 이는 영구히 해의 대상에서 제외된다. 그리고 다음 단계에서는 이에 대해 재검토 할 수 없다. 예를 통해 GA가 조금이라도 받아들여 졌다면 다시 일반적인 내용을 살펴보자.
General Guideline for a GA
GA는 비어 있는 해 집합(solution set)에서 시작하여 집합이 주어진 문제의 instance에 대한 해를 나타낼 때까지 반복을 이용해 순차적으로 해 집합에 항목을 추가한다. 각 반복은 3가지 요소로 구성된다. fig 1도 해당 요소로 구성되어 있으니 빗대어서 확인해보자
- 선택 절차: 부분해 집합에 추가할 다음 항목을 선택한다. 선택은 일부 국소적인(locally) 고려사항을 충족하는 탐욕 기준에 따라 구성된다. (가장 값이 높은 동전으로 거스름돈을 구성하면 동전 개수가 줄어들테니, 현재 가능한 가장 큰 값의 동전을 선택해 부분해 집합에 추가)
- 타당성 확인: 남은 단계를 추가하여 부분 해집합을 완성할 수 있는지 확인하여 새로운 해 집합이 타당한지 판단한다. 즉 부분적으로 생성된 해 집합을 확장하여 전체 해 집합을 얻을 수 있는가?라는 질문의 답에 따라 처리한다. (부분해 집합이 거슬러 줄 금액을 초과하는지 검사. 초과시 가장 최근에 추가한 동전 삭제하고 돌아가서 한 단계 작은 동전 선택)
- 해 검사: 새로운 부분해 집합이 주어진 문제의 instance에 대한 해를 구성하는지 판단(부분해 집합이 거슬러 줄 금액과 일치하는지 검사. 모자라다면 돌아가서 부분해 집합에 추가할 동전을 고름)
이 기술은 각 단계에서 일련의 선택을 통해 최적화 문제에 대한 해 집합을 구성한다. 일부 문제의 경우 GA는 모든 instance에 대해 최적의 해 집합을 산출하나, 대부분의 문제는 그렇지 않다. 그러나 대략적인(근시안적인) 해결책이 필요한 경우에는 유용하다.
Ex2. Minimum Spanning Tree (MST)
이번 예시는 최소비용 신장트리(MST)를 구하는 것이다. 엔지니어가 많은 도시를 도로로 연결하여 누구든지 어느 도시에서나 다른 도시로 운전할 수 있기를 원한다고 해보자. 하지만 도로를 건설할 자금에 한계가 있어 엔지니어가 도로를 적게 건설하여 최소 비용(최적화 문제)으로 도로를 건설하고자 한다.
이러한 문제를 그래프로 표현하여, 그래프의 MST를 생성함으로써 해결할 수 있다. 그래서 해당 문제를 이해하기 위해서는 graph 자료구조에 대한 이해가 필요하다. 어쨌든 MST는 연결된 그래프의 간선만 제거하여 모든 정점이 연결된 상태를 유지하며 나머지 간선들의 합이 최소가 되도록 구성된다. 이에 대해 몇가지 정의하자.
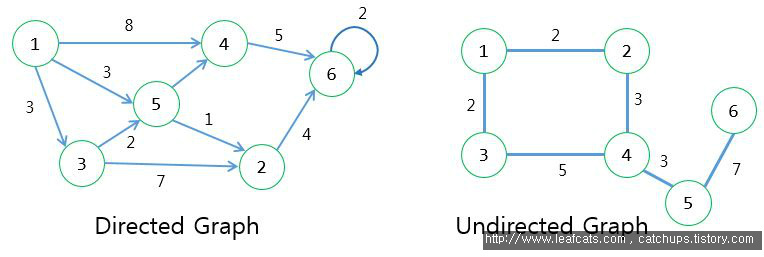
- 모든 정점 쌍 사이에 경로가 있는 경우 이를 무향 그래프(undirected graph)라고 한다.
- 단순 사이클는 처음 정점과 끝정점을 제외하고 중복된 정점이 없는 사이클(시작과 끝이 같음, 경로와 헷갈리지 말자)이다.
- 비순환 그래프는 단순 사이클이 없는 무향 그래프이다.
- 루트 트리(rooted tree)는 비순환, 연결, 무방향 그래프이다.
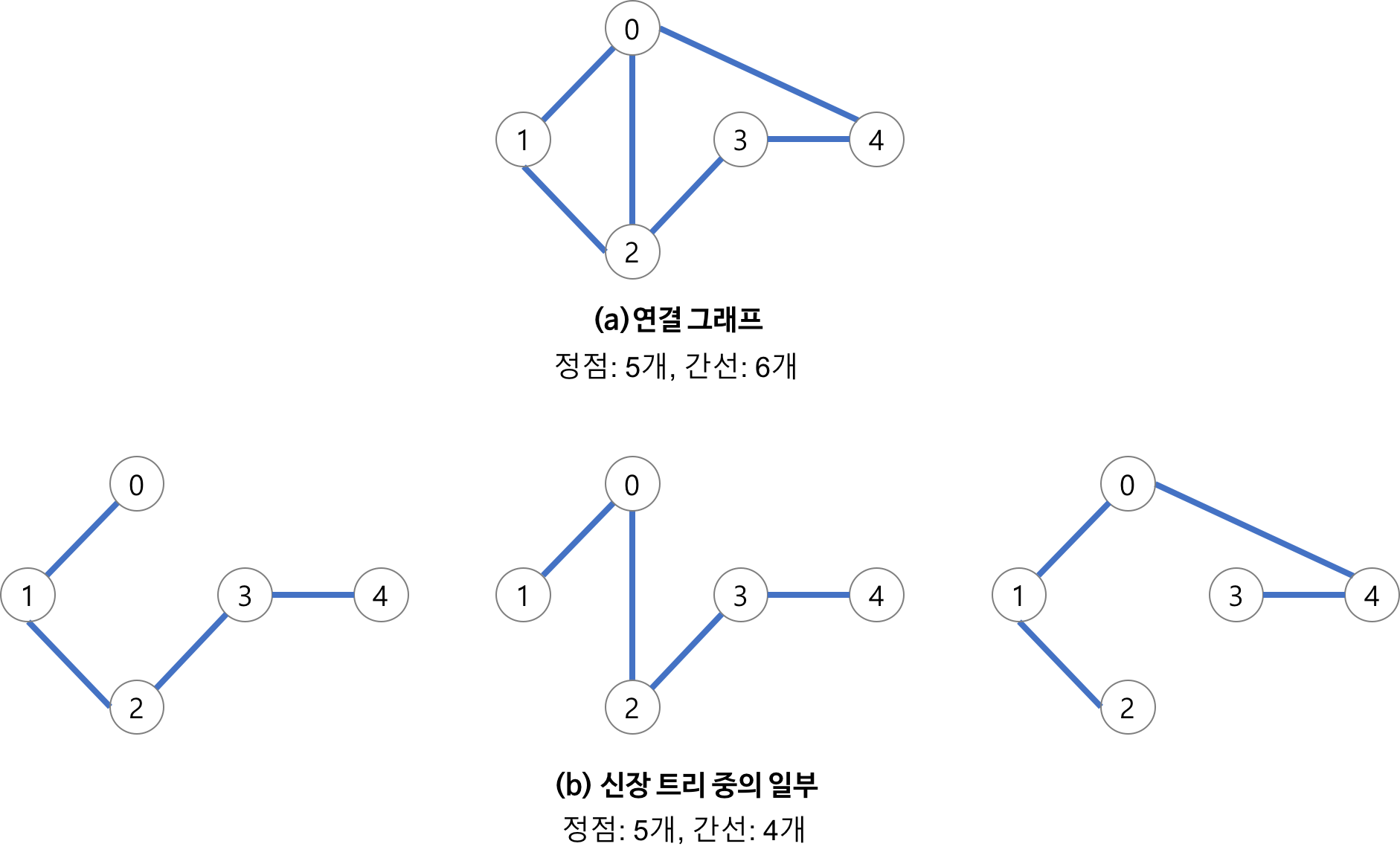
- 그래프 G의 신장 트리는 G의 모든 정점을 포함하는 트리이다.
그래프는 하나 이상의 신장 트리를 가질 수 있으므로 이중에서 최소 가중치를 가지는 신장 트리를 선택(최적화 문제)해야한다. 배경을 쌓았으니 본격적으로 살펴보자.
가중 연결 그래프를 G=(V, E)로, G의 신장 트리를 T=(V, F)라고 하자. V는 정점들의 집합, E는 간선들의 집합, F는 E의 부분집합이다. 이제 알고리즘을 확인해보자.

fig 4를 살펴보자. 우선 신장 트리를 구성하는 간선들이 담길 빈 집합 F를 만들어준다. 그리고 탐욕 기준에 따라 간선을 선택한다(선택 절차). 그리고 선택한 간선을 F에 추가했을 때 사이클이 구성되는지 판단하고 구성되지 않는다면 F에 해당 간선을 추가한다(타당성 확인). 그리고 F가 G의 신장 트리가 되는지 확인한다(해 검사).
위의 알고리즘에서 간선은 탐욕 기준을 사용하여 선택된다고 했는데, 해당 기준을 어떻게 설정해야 할까? 여기서 서로 다른 기준을 사용하는 두 가지 알고리즘을 가질 수 있다. 바로 프림(Prim) 알고리즘과 크루스칼(Kruskal)알고리즘이다.
Prim GA for MST

Prim 알고리즘은 E의 부분집합 F(현재 비어있음)와 \(v_1\)을 포함하는 V의 부분집합 Y={\(v_1\)}가 있는 상태에서 시작한다(X=V-Y라고 하자). 그리고 Y의 정점과 최소 가중치를 갖는 간선으로 연결된 집합 X의 정점 u를 Y에 가장 가까운 정점이라고 정의하자.
이 알고리즘에서는 Y에 가장 가까운 정점 u를 Y에 추가하고 이를 연결하는 간선을 F에 추가한다. 그리고 이 과정은 Y=V가 될 때까지 계속된다. 밑의 코드로 확인해보자.

다음과 같이 코드로 표현할 수 있다. Prim 알고리즘은 간선이 없는 하나의 정점만 존재하는 하위 트리 \(T_1\)으로 시작한다. 이후 한번에 하나의 정점을 추가하여 하위 트리를 점점 확장해나간다(\(T_1 \rightarrow T_2 \rightarrow ... T_n\)). 즉 i번째 반복에서, \(T_i\)에는 없지만 이미 \(T_i\)에 있는 정점에 가장 가까운 새 정점을 추가하여 \(T_i\)에서 \(T_{i+1}\)을 구성한다(Geedy한 단계). 그리고 모든 정점이 트리에 포함되면 중지한다.
처음에 이미 하나의 정점이 포함되어 있는 상태니 총 반복횟수는 n-1이라고 할 수 있다. 좀더 C++형식으로 구제화 된 코드를 살펴보자.

입력으로 받은 정점 개수 n과 graph(2차원 배열)를 이용해 최소 신장 트리를 만드는 알고리즘이다. fig 7에서는 필요한 변수를 선언해주고 적절하게 초기화해준다. nearest[i]는 i 정점과 가장 가까운(가중치가 가장 낮은) 정점을 담는 배열이다. distance[i]는 정점 i와 연결된 간선 중 가장 적은 가중치의 크기가 담기는 배열이다. 처음에는 nearest 배열은 2~n 인덱스까지 모두 1로 초기화해주고, distance 배열은 graph의 첫째행과 같게 해준다.

repeat라는 반복문 안에 두 개의 for문이 존재한다. 첫번째 for문에서는 현재까지의 하위 트리에 속한 정점들과 속해있지 않은 정점들을 연결하는 간선 중 가장 가중치가 짧은 것을 선택하는 과정이다. 이후에 해당 간선을 F에 추가해준다.
두번째 for문에서는 간선을 F에 추가함으로써 새로운 정점이 하위 트리에 추가되는데, 해당 정점과 연결된 다른 정점들 중 가장 적은 가중치를 가지는 정점을 선택하고, 해당 가중치 값과 정점을 distance, nearest에 추가해준다.
Time Complexity of Prim's algorithm
이제 시간 복잡도를 알아보자 반복문으로 구성되어 있어 파악하기에 그리 어렵지 않다. 그래프는 인접 행렬로 표현되며 우선순위 큐는 정렬되어 있지 않은 배열로 구현된다. 그리고 basic operation을 두 개의 반복문(for) 내부에 있는 비교 연산으로 설정하자.
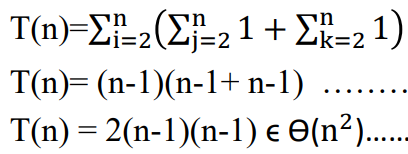
그러면 fig 9처럼 시간 복잡도를 계산할 수 있다. n-1번의 각 반복에서 정렬되지 않은 배열을 탐새하여 최솟값을 찾아 삭제한 다음 나머지 정점의 우선 순위를 업데이트한다.
Kruskal's GA for MST
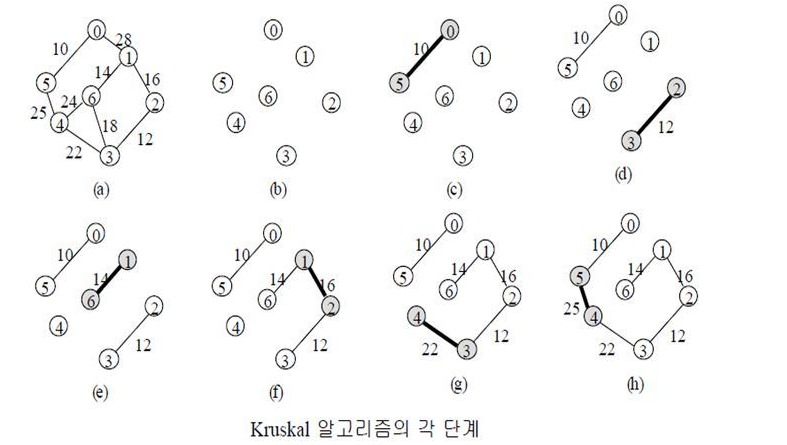
이번에는 MST를 찾는 또다른 알고리즘인 크루스칼(kruskal) 알고리즘이다. prim에서는 하나의 정점만 존재하는 하위 트리로 시작해서 간선을 하나씩 추가해가면서 MST를 구성하였다. 크루스칼 알고리즘에서는 n개의 트리로 시작한다. 여기서 각 트리는 단 하나의 정점으로 이루어져 있다. 이 트리를 단계별로 병합하여 MST를 생성하는 것이다.
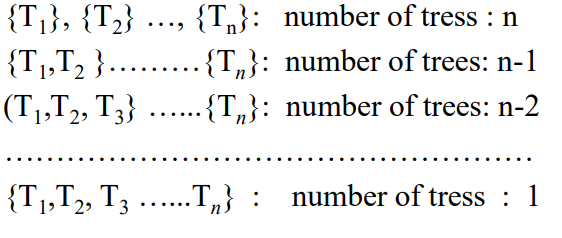
그렇다면 어떤 기준으로 병합하는지 살펴봐야 한다. 우선 그래프를 이루는 간선들의 집합 E를 오름차순으로 정렬한다. 순서대로 해당 간선을 꺼내보면서 해당 간선으로 정점들을 연결했을 때 사이클이 형성되면 해당 간선으로는 연결하지 않고 다음 간선을 확인한다. 이 과정을 반복하면 MST가 생성되는 것이다.
수도 코드로 표현해보면 프림 알고리즘보다 비교적 간단하다.

Time Complexity of Kruskal's Algorithm
해당 알고리즘은 프림과는 달리 instance마다 다른 시간복잡도를 가진다. 운이 좋으면 n-1번의 basic operation만으로도 MST를 형성할 수 있기 때문이다. 하지만 우리가 중요시 해야할 것은 worst-case이다. 정점의 개수를 n, 간선의 개수를 m(\(n-1\leq m\leq \frac{n(n-1)}{n}\))이라고 하고 이를 계산해보자.
우선 basic operation은 간선을 추가했을 때 사이클이 형성되는지 판단하는 comparison instruction이라고 할 수 있다. 그리고 처음에 간선들의 집합(배열)을 정렬할 때 병합 정렬을 사용한다면 이것의 시간 복잡도는 \(w(n)=\theta(mlogm)\)이라고 할 수 있다. 그리고 그래프의 모든 정점을 하나의 정점만을 가지는 n개의 트리로 만드는데에는 \(w(n)=\theta(n)\)이라는 시간 복잡도를 가진다. 하지만 이건 전체 시간 복잡도에 큰 비중을 차지하지 않으므로 무시하자.
최악의 경우는 정점들끼리 모두 연결된 그래프의 모든 간선들을 확인했을 때이다. 이때의 간선의 개수는 \(m=\frac{n(n-1} {2}\)이다. 반복도 m만큼 하니깐 해당과정의 시간 복잡도는 \(\theta(n^2)\)을 가진다. 그럼 전체 시간 복잡도를 구해보면 \(W(m, n)=\theta(n^2log n^2)+n^2=\theta(n^2logn)\)이라고 할 수 있다.
Ex3. Shortest paths from single source to many destinations
이전 DP에 대한 글에서 한 지점에서 다른 지점까지의 최단 경로를 찾는 Floyd 알고리즘에 대해 알아봤다. 그런데 이 알고리즘은 결국 한 지점에서 다른 지점까지의 경로만 구하지 않고 모든 정점에서 다른 정점까지의 최단 거리(+경로)를 모두 알아내었다. 때문에 \(n^3\)이라는 매우 큰 시간 복잡도를 가지게 된다.
만약 우리가 원하는게 하나의 정점에서 다른 여러 정점까지의 최단 경로만 알아야 할 경우에는 Floyd 알고리즘은 적절치 않을 것이다. 때문에 더 효율적인 GA를 활용하는 다익스트라(Dijkstra) 알고리즘이 개발되었다. 이 알고리즘은 주어진 출발지 정점에서 모든 목적지 정점까지의 경로가 있다고 가정한다. 때문에 다익스트라 알고리즘은 MST를 구성하는 prim 알고리즘과 유사하다.
다익스트라 알고리즘은 간선의 가중치가 음이 아닌 유향&무향 그래프 모두에 적용가능하다. 다익스트라 알고리즘은 주어진 정점(source)에서 모든 정점(destination)까지 거리의 오름차순으로 최단 경로를 찾는다. 먼저 source에 가장 가까운 정점에 대한 최단 경로를 찾은 다음 두 번째로 가까운 정점에 대한 두 번째 경로를 찾는 식이다. 따라서 i번째 반복이 시작되기 전에 동일한 source에 가장 가까운 i-1개의 정점이 식별된다.
Summary of Dijkstra's Algorithm
한 정점에서 모든 정점으로 가는 경로의 집합을 가지게 되며, 아래 fig 13과 같이 공통된 간선을 가질 수 있다.
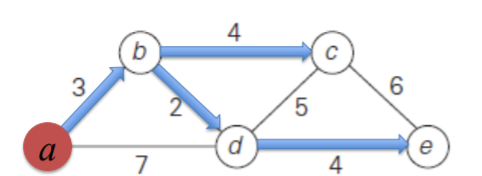
그렇게 하기 위한 과정은 다음과 같다.
- source를 설정
- source를 기준으로 각 정점의 최소 비용을 저장
- 방문하지 않은 정점에 연결된 간선 중 가장 가중치가 적은 간선 선택
- 해당 정점을 거쳐서 갈 수 있는 경우를 고려하여 최소 비용 갱신
- 모든 정점에 대한 최단 거리를 알 때까지 3~4과정 반복
매 반복마다 다익스트라 알고리즘은 경로의 길이를 비교하고 간선의 가중치를 추가해야 하는 반면, 프림 알고리즘은 주어진 간선의 가중치만 비교하였다.
Code of Dijkstra's Algorithm
2단계에 걸쳐 다익스트라 알고리즘을 수도 코드로 확인해보자.
F = {};
Y = {v1};
while(instance가 해결되지 않는 동안)
{
//선택 및 타당성 확인(no cycle formation)
1. 집합 V의 정점을 중간 정점으로 사용하여 v1에서 가장 짧은
경로를 가지는 집합 X에서 새 정점 u를 선택
2. 새로운 정점 u를 집합 Y에 추가
// solution 검사
if(Y=V)
해당 instance 해결 됨
}fig 13을 예시(index가 0이 아닌 1부터 시작)로, 조금 더 자세한 코드를 살펴보자.
void dijkstra(int n, const number W[][], set_of_edges& F)
{
index i, vnear;
edge e;
index touch[2..n];
number length[2..n];
F = null;
for(i=2; i<=n; i++){
touch[i] = 1;
length[i] = W[1][i];
}
repeat(n-1 times){ // Add all n-1 vertices to Y
min = inf;
for(i=2; i<=n; i++) // Check each vertex for
if(0 <= length[i] < min){ // having shortest path
min = length[i];
vnear = i;
}
e = edge from vertex indexed by touch[vnear] to vertex indexed by vnear;
add e to F
for(i=2; i<=n; i++)
if(length[vnear] + W[vnear][i] < length[i]){
length[i] = length[vnear] + W[vnear][i];
touch[i] = vnear; // For each vertex not in Y
} // update its shortest path.
length[vnear] = -1; // add vertex index by vnear to set Y
} // end of repeat
} // end of DijkstraProblem은 a에서 모든 정점까지의 최단 경로를 구하는 것이다. 이에 대한 input은 정점의 개수 n, 그래프 W[][]이고, output은 a에 대한 최단 경로가 담긴 F이다.
우선 첫번째 반복문에서는 최단 경로로 i번째 정점에 가기위해 거치는 가장 최근 정점이 담기는 touch배열은 1로, a에서 정점 i까지의 최단거리가 담길 length 배열은 W의 1행 i열의 값으로 초기화 해준다. fig 13같은 경우에는 [0, 3, inf, 7, inf] 형식으로 저장될 수 있다. F는 처음에는 아무것도 없다.
repeat에서 본격적으로 다익스트라 알고리즘이 적용된다. n-1번 반복한다는 것은 Y에 n-1개의 정점을 모두 넣을 때 까지 반복한다는 뜻이다. min을 무한대로 설정한 뒤 첫번째 for문이 시작된다. 해당 반복문에서는 각 정점에 최단 경로가 존재하는지 확인한다. 현재 length = [0, 3, inf, 7, inf]이므로 해당 반복문이 완료되면 min = 3, vnear = 2가 된다.
e는 touch[vnear] = 1, vnear = 2를 연결하는 간선이다. 해당 간선을 F에 추가한다.
repeat의 두번째 for문을 살펴보자. 현재 length에는 정점 a만을 거쳐서 갈 수 있는 최단 거리가 담긴다. 이제 F에 e가 추가됨으로써 정점 b를 거칠 때, 더 적은 가중치를 가지는 경우를 고려해야 한다. 예를 들어 현재는 a-c까지의 거리는 inf로 설정되어 있다. 하지만 b를 거치게 된다면 3+4의 가중치를 가지므로 length[3] = 7로 갱신되어야 한다. 그리고 b를 거치게 되면 a에서 바로 d로 갈 때의 가중치 7보다 더 적은 5의 가중치가 요구된다. 때문에 length[4] = 5로 갱신된다. 즉 위에서 설명했던 '해당 정점을 거쳐서 갈 수 있는 경우를 고려하여 최소 비용 갱신'이 해당 반복문에 해당한다.
Time complexity of Dijkstra's algorithm
그래프는 인접 행렬로 표현되고 우선순위 큐는 정렬되지 않은 배열로 구현된다. 그리고 기본 연산은 위 코드에서는 repeat내 두개의 반복문에 있는 비교 연산이다. 두 개의 반복문은 각각 n-1번 실행된다.
그러므로 시간 복잡도는 \(T(n)=\sum_{n}^{i=2}(\sum_{n}^{j=2}1+\sum_{n}^{k=2}1)=(n-1)(2n-2)\in \theta(n^2)\)
자료 출처
- Introduction to The Design and Analysis of Algorithms / Ananu Levitin
- FOUNDATIONS OF ALGORITHMS / RICHARD E. NEAPORITAN
- fig 3, 5 / https://gmlwjd9405.github.io/2018/08/28/algorithm-mst.html
- fig 11 / https://eehoeskrap.tistory.com/39
'알고리즘 > 수업 복습' 카테고리의 다른 글
| Backtracking Algorithm Design Method (백트래킹 알고리즘) (1) | 2021.11.22 |
|---|---|
| Greedy Algorithm Design Pattern 2(탐욕 알고리즘) (0) | 2021.11.08 |
| Dynamic Programming Design Pattern (동적 계획법) (0) | 2021.10.13 |
| Divide and Conquer design pattern(분할정복) (0) | 2021.10.04 |
| Algorithm Efficiency(알고리즘 효율성) (0) | 2021.09.18 |




댓글