이번에 알아볼 알고리즘 기법은 분기 한정법(Branch and Bound Method)이다. 이 글에서는 최적화 문제를 해결하기 위한 분기 한정 방법, 비슷한 기법인 역추적 기법과의 차이점을 알아볼 것이다. 그리고 어떤 문제가 분기 한정법을 사용하기에 적절한 문제인지 식별해보고, 이전 부터 계속 해왔던 0/1 배낭 문제를 해당 기법을 이용하여 해결해 볼 것이다.
Introduction to Branch and Bound
역추적 알고리즘과 마찬가지로 분기 한정 알고리즘도 상태 공간을 사용하여 조합 문제를 해결한다. 그러나 분기 한정법은 방문할 다음 노드가 런타임 중에 결정되고 입력 인스턴스마다 다르기 때문에 트리 탐색 순서를 미리 결정하지 않는다. 또한 역추적 알고리즘은 최적화/비최적화 문제를 모두 해결할 수 있으나, 분기 한정 알고리즘은 최적화 문제만 해결하도록 설계되었다.
역추적에서의 promising function에서는 부울 값을 사용했지만, 분기 한정법의 promising function에는 숫자 값을 사용한다. 해당 수치는 노드를 넘어 확장하여 얻을 수 있는 해의 값에 경계(bound)를 얻기 위해 사용된다. 경계 값이 지금까지 찾은 최적 값보다 좋지 않으면 해당 노드는 유망하지 않고, 그렇지 않으면 해당 노드는 유망하다. 역추적 알고리즘과 분기 한정 알고리즘의 유사점과 차이점을 정리하면 다음과 같다.
| 역추적 | 분기 한정 | |
| 유사점1 | 상태 공간 트리를 사용하여 문제 해결 | |
| 유사점2 | 최적화 문제의 경우, 이론적 상한이 각 노드에서 계산되어 유망성을 결정 | |
| 유사점3 | worst-case일 경우네는 기하급수적(exponential) 시간 복잡도를 가짐 | |
| 차이점1 | 깊이 우선 탐색(DFS) 트리 순회라고 하는 미리 결정된 순서로 트리 탐색 | 트리에서 방문하는 다음 노드는 많은 유망 노드 중 가장 좋은 유망 노드를 선택하여 런타임 동안 결정된다. 이는 너비 우선 탐색이 수정된 최상 우선 탐색이 사용됨 |
| 차이점2 | 최적화 및 비 최적화 문제에 사용 | 최적화 문제에만 사용 |
Breadth First Search
분기 제한 알고리즘은 너비 우선 탐색(BFS, Breadth First Search)을 수정한 최상 우선 탐색(Best First Search)을 구현한다. 때문에 BFS에 대해 먼저 간단히 알아보자.
BFS에서는 루트 노드를 먼저 방문하고 fig 1.1에 표시된 대로 level-1의 모든 노드를 방문한 다음 level-2의 모든 노드를 방문하고 마지막으로 level-n의 모든 노드를 방문한다. 때문에 깊이 우선 탐색과 달리 단순 재귀 알고리즘이 없고 스택(FILO) 대신 큐(FIFO) 자료구조를 사용하여 구현 할 수 있다.

Pseudocode of BFS
Without Pruning
void breadth-first-tree-search(tree T){
queue_of_node Q;
node child, parent;
initialize(Q); //initialize queue to be empty
parent = root of T;
visit parent;
enqueue(Q, parent); //insert parent at the end of Queue
while(!empty(Q)){
dequeue(Q, parent); //remove from front queue
for(each child child of parent){
visit child;
enqueue(Q, child)
}
}
}다음은 분기 한정에서의 가지 치기가 사용되지 않은 일반적인 BFS이다. 큐를 사용하는데 enqueue를 이용해 큐의 가장 뒤에 아이템을 위치시키고 dequeue를 이용해 큐의 가장 앞의 아이템을 제거한다. 코드를 살펴보면 fig 1.1같은 순서로 트리를 탐색한다.
With Branch and Bound Pruning
void breadth_first_branch_and_bound(state_space_tree T, number& best){
queue_of_node Q;
node c, p; //child node and parent node
initialize(Q); //Initialize Q to be empty
p = root of T; //Visit root
enqueue(Q, p); //add p at the end of queue Q
best = value(p); //value() function to extract actual value at node P
While(!empty(Q)){
dequeue(Q, p);
for(each child c of p){
if(value(c) is better than best), then best = value(C);
if(bound(c) is better than best), then enqueue(Q, c); //add to Q
}// bound() function to extract theoretical value at node P
}
}//end다음은 분기 한정법의 가지 치기를 이용해 위의 BFS를 수정한 것이다. 여기서는 노드의 한계값이 현재 최적 해의 값보다 좋은 경우에만 그 노드에서 계속 트리를 확장한다.
0/1 Knapsack problem with Branch and Bound
이제 0/1 배낭 문제에 분기 한정법을 적용해보자. 위에서 본 분기 한정법을 사용하는 가지치기 알고리즘은 재귀 함수를 사용하지 않으므로, 각 재귀 호출에 생성되는 새 변수가 없다. 따라서 0/1 배낭 문제에 대해 다음과 같은 노드 구조를 사용하여 각 노드에 필요한 정보를 저장해야 한다.
struct node{
int level; //the level of the node in the tree
int profit; //the profit of the node
int weight; // the weight of the node
};다음과 같은 노드 구조를 이용하면 다음과 같은 알고리즘을 사용할 수 있다. 우선 BFS를 이용한 경우이다.
//inputs: n, W, decreasing order sorted array w[] and p[] by p[i]/w[i]
//output: Maimum profit
void knapsack2(int n, const int p[], const int w[], int w, int& maxprofit){
queue_of_node Q;
node c, p;
initailize(Q); //Initialize Q to be empty
p.level = 0; p.profit = 0, p.weight = 0; maxprofit = 0; // Initialize p to root
enqueue(Q, p);
while(!empty(Q)){
dequeue(Q, p); //remove p from Q
c.level = p.level + 1; // Set c to a child of p
//Set c to the child that includes the next item
c.weight = p.weight + w[c.level]
c.profit = p.profit + p[c.level]
if(c.weight <= W && c.profit > maxprofit)
maxprofit = c.profit;
if(bound(c) > maxprofit)
enqueue(Q, c)
//Set c to the child that does not include the next item
c.weight = p.weight;
c.profit = p.profit;
//no need to compare c.profit with maxprofit
if(bound(c) > maxprofit)
enqueue(Q, c);
}//end of while loop
}//end of knapsack2다음과 같은 알고리즘에 저번 글(지금 말할 내용들과 비교해보자)에서의 0/1 배낭문제에서 사용된 것과 동일한 인스턴스를 넣어주면 fig 2.1과 같은 상태 공간 트리가 얻어진다.

Compare with DFS Backtracking Pruning
역추적 방법의 가지치기와 비교해보자. 우선, 노드(3,1)과 노드(4,3)의 경계값은 0이다. 왜냐하면 노드의 weight가 W보다 크거나 같아 해당 노드가 non-promising일 때 경계값은 0으로 재설정되기 때문이다. 즉,
둘째, 역추적의 경우 node(1,2)는 유망하지 않다. 그러나 이때의 최대 이익(maxprofit)의 값이 $40이고 해당 노드의 경계값은 $82이기 때문에 BFS의 세번째 반복에서는 해당 노드를 방문해서 유망하다고 처리한다.
셋째, 노드의 자식 방문 여부는 해당 노드를 방문하는 시점에 결정된다. 예를 들어 노드(2,3)을 방문할 때 현재 최대 이익이 $70인데 경계값이 $82이기 때문에 해당 노드의 자식을 방문하기로 결정한다.
그리고 DFS때와 달리 BFS에서는 노드의 자식을 방문할 때 최대 이익이 변경될 수 있다. 예를 들어 노드(2,3)의 자식을 방문할 때 최대 이익이 $70에서 $90으로 변경되었다.
이처럼 BFS를 이용한 접근 방식은 각 노드의 자식을 확인하기 때문에 시간을 낭비한다. 때문에 여기서 더 개선된 최상 우선 탐색을 사용하여 이러한 과정을 피할 수 있다.
Using Best-First search with Branch and Bound Pruning
위에서 봤듯이 일반적으로 역추적 알고리즘에 사용되는 DFS에 비해 지금 사용했던 BFS가 더 나은 점이 없다. 두 가지 모두 미리 결정된 순서로 맹목적으로 진행되기 때문이다. BFS는 트리의 두 개 이상의 확장되지 않은 유망 노드의 경계 값을 비교하여 향상될 수 있다.
따라서 주어진 노드의 모든 자식을 방문한 후, 우리는 확장되지 않은 노드 중에서 가장 좋은 경계 값을 가진 하나의 노드를 선택하여 확장할 수 있다. 결과적으로 위에서 언급한 최상 우선 검색을 사용하여 트리를 확장하는 것이다. 그 과정을 코드로 나타내면 다음과 같다.
void best_first_branch_and_bound(tree T, number& best){
priority_queue_of_node PQ;
node c, p;
initailize(PQ); //Initialize PQ to be empty
p = root of T; best = value(p);
insert(PQ, p); //function to add
while(!empty(Q)){
remove(PQ, p); //function to remove node with best bound
if(bound(p) is better than best){//Check if node is still promising
for(each child c of p){
if(value(c) is better than best), then best = value(c);
if(bound(c) is better than best), then insert(Q, c);
}
}
} //end of while
} //end of best-first각 삽입/제거 시간에 노드에 대한 경계 값이 필요하고 우선 순위 큐에 있는 노드의 순서를 지정하기 위해 노드에 경계 값을 저장해야한다. 때문에 노드는 다음과 같은 구조를 가진다.
struct node{
int level; //the level of the node in the tree
int profit; //the profit of the node
int weight; // the weight of the node
float bound;
};이제 이 노드와 최상 우선 검색을 이용하여 개선된 0/1 배낭 문제 해결 알고리즘을 살펴보자.
//inputs: n, W, decreasing order sorted array w[d] and p[] by p[i]/w[i]
//output: Maximum profit
void knapsack3(int n, int p[], int w[], int W, int& maxprofit){
priority_queue_of_node PQ;
node c, p;
initailize(PQ); //Initialize PQ to be empty
p.level = 0; p.profit = 0; p.weight = 0; maxprofit = 0; //Initialize p to root
p.bound = bound(p);
insert(PQ, p); // this function adds node to PQ
while(!empty(PQ)){
remove(PQ, p) //this function remove node with best bound
if(p.bound > maxprofit){ //check if node is still promising
//Set c to a child that includes next item
c.level = p.level+1; c.weight = p.weight + w[c.level];
c.profit = p.profit + p[c.level];
if(c.weight <= W && c.profit > maxprofit) then maxprofit = c.profit;
if(c.bound > maxprofit) then insert(PQ, c);
//Set u to the child that does not include the next item
c.weight = p.weight;
c.profit = p.profit;
c.bound = bound(u);
if(bound(u) > maxprofit), then insert(PQ,c);
} //end of outer if in previous slide
} //end of while loop in previous slide
} //end of knapsack3 in previous slide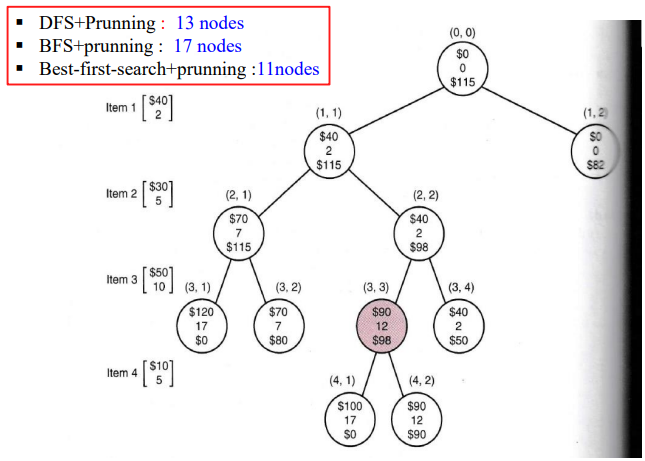
같은 인스턴스를 넣어줬을 때 최상 우선 탐색을 사용한 분기 한정 알고리즘(knapsack3)이 가장 적은 노드를 탐색했음을 확인할 수 있다. 한번 이전 일반적인 BFS를 사용햇던 knapsack2 알고리즘과 비교해보자.
최상 우선 탐색에서는 PQ에서 노드를 제거한 후 경계 값을 전역 변수 maxprofit보다 높은지 확인한다. 이 값이 false라면 방문했던 노드가 유망하지 않게 된다. 예를 들어 노드(1,2)는 처음 방문할 때는 유망하나 나중의 maxprofit이 90이 되면 더 이상 유망하지 않게 된다. 이렇듯 방문 후 유망에서 비 유망으로 변경되는 노드의 자식 방문을 피하는 것이다.
주어진 노드의 모든 자식을 방문한 후 우리는 확장되지 않은 모든 유망 노드를 살펴본 다음 가장 좋은 경계 값을 가진 노드를 확장할 수 있다. 이렇게 하면 미리 정해진 순서대로 맹목적으로 확장하는 것보다 더 빨리 최적 해에 도달할 수 있다. 따라서 최상 우선 탐색은 방문 후 유망하지 않게 될 노드의 자식을 방문하는 걸 방지한다.
자료 출처
- Introduction to The Design and Analysis of Algorithms / Ananu Levitin
- FOUNDATIONS OF ALGORITHMS / RICHARD E. NEAPORITAN
- Panda의 IT 노트 / https://seungjuitmemo.tistory.com/109
'Computer Science > 알고리즘' 카테고리의 다른 글
| More Computational Complexity theory of a problem :The searching Algorithm (0) | 2021.12.21 |
|---|---|
| Introduction to Computational Complexity theory of a Problem: The sorting Algorithm Problem (0) | 2021.12.13 |
| Backtracking Algorithm Design Method (백트래킹 알고리즘) (1) | 2021.11.22 |
| Greedy Algorithm Design Pattern 2(탐욕 알고리즘) (0) | 2021.11.08 |
| Greedy Algorithm Design Pattern 1(탐욕 알고리즘) (0) | 2021.10.19 |




댓글