Backtracking Algorithm Design Method (백트래킹 알고리즘)

  이번에는 백트래킹 알고리즘에 대해 알아보자. 이 글에서 알아볼 것은 다음과 같다.

• 백트래킹 기술 설명
• 백트래킹 기법이 문제 해결에 적절한 접근 방식인지 판단
• 주어진 문제에 대한 상태 공간 트리 정의
• 주어진 문제에 대한 상태 공간 트리의 노드가 유망(promising)하거나 비유망(non-promising)한 경우 정의
• 상태 공간 트리를 제거하는 알고리즘 생성
• 주어진 문제를 해결하기 위해 백트래킹 기법을 적용하는 알고리즘 생성

  여기서 상태 공간 트리(state-space-tree)란 문제 해결의 중간 상태를 각각 한 노드로 나타낸 트리이다.

※ P, NP Problem

  백트래킹을 살펴보기 전에 P, NP에 대해 간단히 짚고 넘어가자. 이제 막 알고리즘에 대해 배우고 있는 입장에서 명확히 이해하기 어려운 개념이므로 꼭 따로 찾아봤으면 한다. 짧게 말하자면 P는 해당 문제를 다항 시간에 해결할 수 있는 알고리즘이 존재하는 결정 문제의 집합이다. 우리가 이전에 했던 이진 탐색, 퀵 정렬, 피보나치 등을 생각해보자.

  NP는 해당 문제를 해결하는 non-deterministic 다항 시간 알고리즘이 존재하는 최적화 문제의 집합이다. 쉽게 말하면 직접 문제의 해를 구해야 알고리즘의 수행시간을 판단할 수 있는 문제들이다. 이에 대한 예시는 밑에서 확인해볼 것이다.

Overview of Backtracking Method

  백트래킹은 일부 기준을 충족하도록 지정된 개체 집합에서 개체의 시퀀스가 선택되는 문제를 해결하는데 사용된다. 쉽게 말하면 해를 찾다가 막히면 다시 되돌아가서 다시 해를 찾는 것이다.

  백트래킹은 트리의 DFS(깊이 우선 탐색)의 수정된 버전이다. 전위 순회라는 DFS 방법 중 하나가 있는데 부모 노드->왼쪽 자식 노드 -> 오른쪽 자식 노드로 탐색을 수행하는 방법이다. DFS에서는 막다른 길에 도달할 때까지 경로를 깊이 따라 간다. 막다른 길을 만난다면 방문하지 않은 자식이 있는 노드에 도달할 때까지 위쪽으로 역추적(backtracking)다음 다시 깊이 이동한다.

  일반적으로 백트레킹은 상태 공간 트리의 DFS를 수행하여 각 노드가 유망한지 확인하고, 비유망이면 노드의 부모 노드로 돌아가서 다음 자식의 탐색을 진행한다. 이러한 과정을 가지치기(pruning)라고 한다. 방문한 노드로 구성된 하위 트리를 정리된 상태 공간 트리(pruned state space tree)라고 한다. 요약하면 백트래킹은 다음과 같은 단계를 따른다.

1. 해 공간에 대한 트리 모델을 시각화한다.
2. 가지치기 메커니즘을 만든다

  해당 과정을 통해 우리는 하나(하나의 해)또는 여러개(여러개의 해)의 말단 노드에 도달하게 된다.

Example of DFS

fig 1

  fig 1의 트리를 예로 들어 DFS로 모든 노드를 탐색해보자. 좀전에 말해듯이 부모 노드->왼쪽 자식 노드->오른쪽 자식 노드로 탐색을 진행해야한다. 이러한 방법과 유사하게 백트래킹 알고리즘도 해를 찾다가 일부 기준을 충족하지 못하면 다시 되돌아가서 해를 찾는 것이다.

Ex1. N-Queens problem Using backtracking

fig 2.1

  체스에는 퀸 이라는 말이 있는데 퀸은 상하좌우, 대각선 방향으로 제한없이 이동할 수 있다. 주어진 문제는 n개의 퀸을 n*n 체스판에 배치했을 때 퀸들이 서로를 공격할 수 없는 경우를 구하는 것이다. 정리하자면 아래와 같다.

• 서로 동일한 행과 열에 배치되지 않기
• 서로 위쪽, 아래쪽 대각선에 배치되지 않기

  이 문제에서 찾아야 하는 시퀀스는 퀸을 배치하는 n개의 위치이다. 이러한 위치는 \(n^2\)개의 위치 중에서 선택될 수 있고 이중에서 n개의 위치를 특정해야 하는 것이다.

  그럼 N=4라고 해보자. 그렇다면 보드는 16개의 위치를 가지게 된다. 두 퀸이 같은 행에 있을 수 없으므로 각 퀸에 다른 행을 할당하고 어떤 열 조합들이 해를 제공하는지 확인하여 문제를 해결할 수 있을 것이다. 각 퀸은 할당된 행의 4칸 중 한 곳에 위치할 수 있다. 따라서 \(4^4=256\)개의 정답 후보들이 존재한다.

fig 2.2

  이를 트리로 구성하면 fig 2.2와 같고 이러한 트리를 상태 공간 트리라고 한다. 첫번째 퀸(행1)의 열 선택은 레벨 1의 노드들에 저장, 두번째 퀸(행2)의 열 선택은 레벨 2의 노드들에 저장, ... 이런식으로 노드들이 생성된다면 총 256개의 노드로 트리가 구성될 것이다.

  무식하게 모든 경우를 고려할 수도 있지만 당연히 최선이 아닐 것이다. 때문에 우리는 몇가지 기준을 세워야하고 이에 따라 256개의 노드들을 2가지 유형으로 분류해야 한다.

• 비유망 노드(non-promising node): 해결책으로 이어질 가능성이 없는 노드(더 나아갈 이유가 없음)
• 유망 노드(promising node): 해결책으로 이어질 가능성이 있는 노드(더 나아갈 필요가 있음)

  위에서 살펴본 전통적인 DFS는 막다른 곳에 도달할 때까지 모든 경로를 따른다. 여기서는 어떠한 기준(기호, sign)도 고려하지 않는다. 그러나 백트래킹에서는 기준을 기호로 사용하여 DFS의 효율성을 높인다. 해를 찾기 위해 왼쪽 경로부터 순서대로 모든 경로(후보 해)를 확인하고 기준을 사용하여 트리를 가지치기한다. 우선 최적화 되지는 않았지만 단순한 알고리즘부터 살펴보자.

fig 2.3

  처음 p는 루트 노드이고 노드 p를 스택에 push한 다음 확인하는 것이다. 노드 p를 방문할 때, 먼저 유망한지를 판단한다. 만약 노드가 유망하고 p에 해가 있다면 해당 해를 출력한다. p가 유망하지만 해당 노드에 해가 없는 경우에는 자식 노드를 방문한다. p가 유망하지 않으면 스택에서 해당 노드를 pop하고 부모 노드로 돌아가서 다른 형제 노드로 탐색을 진행한다. 일부 어플리케이션에서는 말단 노드에 도달하기 전에 해를 찾을 수도 있다. 그리고 상태 공간 트리는 명시적으로 존재하지 않고 묵시적으로 존재한다.

fig 2.4

  fig 2.4를 보면 알겠지만 백트래킹을 사용하면 해를 찾기 전까지 27개의 노드만을 확인한다. 하지만 DFS를 사용한다면 155개의 노드를 확인했어야 했다.

  백트레킹이 DFS보다 훨씬 효율적이라는 것은 알게됐다. 그렇다면 이제는 fig 2.3의 Promising()을 어떻게 구현해야하는지 생각해 봐야한다. ci, ck를 각각 i, k번째 행의 여왕이 위치한 열이라고 하고 col(i), col(k)로 표시하자. col(i) = col(k)이면 동일한 열이므로 공격가능, col(i)-col(k)=i-k이면 왼쪽 대각선으로 공격 가능, col(i)-col(k)=k-i이면 오른쪽 대각선으로 공격가능하다. 이를 이용하여 밑의 fig 2.5같은 알고리즘을 세울 수 있다.

fig 2.5

  queens 함수의 for문은 (i+1)번째 행의 퀸이 n개의 열 각각에 위치할 수 있는지 확인한다. promising에서는 i번째 행에 위치한 퀸이 1~i-1번째에 위치한 퀸한테 공격받을 수 있는지 판단하여 공격 당할 수 있으면 switch를 false, 당할 수 없으면 true로 하여 해당 값을 반환한다. false라면 상태 공간 트리의 해당 분기에서 더 깊게 들어가지 않게 되고 true라면 더 깊게 들어간다.

Time complexity of queens() Algorithm

   n(퀸의 수)에 대한 함수로 노드의 수를 결정해야 하기 때문에 이론적으로 queen() 알고리즘을 분석하기는 어렵다. 어쨌든 몇가지 접근법을 확인해보자.

  접근법1은 전체 상태 공간 트리에서 노드의 수를 세어 알고리즘의 상한값을 구하는 것이다. 레벨 0에서 노드의 개수는 1(\(n^0=1\))이고, 레벨 1에서 노드의 개수는 n(\(n^1=n\)), ... 이므로 레벨 n에서의 노드 개수는 \(n^n\)이다. 그렇다면 전체 노드의 개수는 \(1+n+...+n^n=\frac{n^{n+1}-1}{n-1}\)이다. 만약 n=8이라면, 상태 공간 트리는 19,173,961개의 노드를 포함하게된다. 결과를 보면 알겠지만 이 방법은 많은 노드를 확인하지 않는 백트래킹의 목적에 맞지 않기 때문에 큰 가치가 없다.

  접근법2는 정사각형 보드에 퀸을 배치하기 위한 행과 열의 제약 조건을 고려하여 유망한 노드의 수를 계산하여 알고리즘의 상한을 찾는 것이다. 레벨 0에서 노드의 개수는 1(\(n^0\), start node)이고, 레벨 1에서 노드의 개수는 n(\(n^1=n\), 첫번째 퀸은 n개의 열에 위치 가능)이다. 두번째 퀸은 n-1개의 열에 위치할 수 있으므로 레벨 2에서 노드의 개수는 (n-1)n이다. 그러므로 레벨 n에서의 노드의 개수는 \(1*...*(n-1)*(n)=n!\)이다. 그러므로 가능한 최대 유망한 노드 개수는 \(1+n+n(n-1)+...+n!\)이다. n=8이라면 최대 109.601개의 유망한 노드가 있을 수 있는 것이다. 그런데 이 방법은 대각선 제약 조건을 고려하지 않고 행/열 제약 조건만을 고려했기에 이 역시 좋다고 볼 수 는 없다. fig 2.6에서 확인할 수 있듯이 유망한 노드의 올바른 수는 이보다 더 적다.

fig 2.6

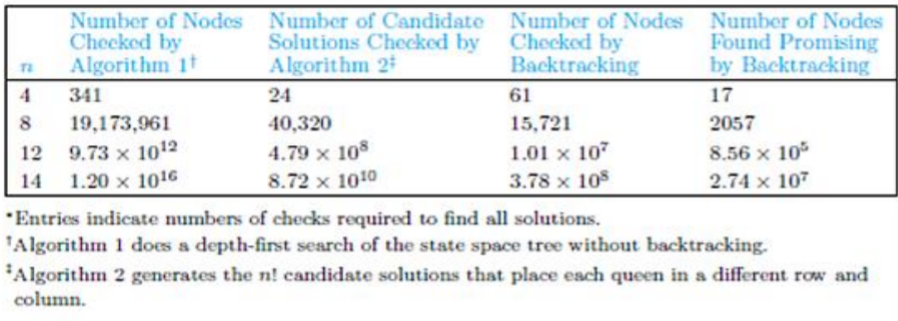
  이처럼 같은 문제임에도 각각의 인스턴스가 다른 시간 복잡도를 가진다. 이러한 최적화 문제는 NP에 속한다.

Summary: Principles of Backtracking Algorithm

  백트래킹의 주요 아이디어는 해를 한번에 하나의 구성요소로 구성하고 다음과 같이 부분적으로 구성된 후보를 평가하는 것이다. 번역하니 뭔가 이해하기 어려운 문장이 되긴했는데 위에서 감을 잡았으면 무슨 말인지 대략 이해가 되는듯 하다...

• 문제의 제약 조건을 위반하지 않고 부분적으로 구성된 해를 추가로 개발 할 수 있는 경우 다음 구성 요소에 대해 나머지 합법적인 옵션을 선택하여 수행된다.
• 다음 구성 요소에 대한 합법적인 옵션이 없는 경우 알고리즘은 부분적으로 구성된 해의 마지막 구성 요소를 다음 옵션으로 대체하기 위해 역추적(백트래킹)한다.
• 상태 공간 트리를 구성하여 백트래킹을 구현한다.
• 이 트리의 루트는 검색 프로세스를 시작하기 전의 초기 상태를 나태낸다.
• 상태 공간 트리는 DFS를 사용하여 구성된다.
• 트리의 첫 번째(두번째, 세번째, ...) 레벨의 노드는 해의 첫번째 구성 요소(두번째, 세번째, ...)에 대한 선택을 나타낸다
• 부분적으로 구성된 해가 완전해로 이어지는 경우의 노드는 유망하다.
• 말단 노드는 알고리즘의 막다른 골목 또는 완전해를 나타낸다.
• 현재 노드가 유망한 경우 해의 다음 구성 요소에 대해 첫번째로 남아 있는 합법적인 옵션을 추가하여 해당 노드의 자식이 생성한다.
• 그렇지 않다면, 알고리즘은 노드의 부모로 역추적하여 마지막 구성 요소에 대한 다음 가능 옵션을 고려한다.
• 마지막으로 알고리즘이 완전해에 도달하면 하나의 해만 필요한 경우 중지하고, 아니면 다른 가능한 해를 계속 검색한다.

  백트래킹 알고리즘은 정확한 해를 찾는 효율적인 알고리즘이 없는 다양한 조합 문제에 사용된다. Brute Force는 주어진 문제의 모든 경우에 대해 매우 느리지만 백트래킹은 부분적으로 구성된 해의 상태를 평가하여 백트래킹에 대한 아이디어를 더욱 향상시킬 수 있기 때문에 최적화 문제에 대해 허용 가능한 시간 내에 적당한 크기의 입력을 갖는 일부 인스턴스를 해결할 수 있다.

  역추적 알고리즘은 NP 문제의 모든 인스턴스에 대해 효율적인 알고리즘은 아니다. 최악의 경우 주어진 문제에서 가능한 모든 후보를 생성하면서 상태공간이 기하급수적으로 증가할 수 있기 때문이다. 우리는 시간, 메모리가 부족해지기 전에 상태 공간 트리의 분기를 충분히 가지치기하기를 희망하며 백트래킹 알고리즘을 사용한다. 그러므로 백트래킹 전략의 성공 여부는 문제마다 다르고 심지어 동일한 문제의 다른 경우에도 다르다. 백트래킹을 적용할 수 있는 다른 예시를 살펴보자.

Ex2. The Sum-of-Subsets Problem

  0/1 knapsack 문제와 유사하다. 도둑이 훔칠 수 있는 상품의 집합이 있고 각 상품에는 고유한 무게와 가격이 있다고 가정하자. 배낭에 들어 있는 항목의 총 중량이 W를 초과하면 배낭이 망가진다. 그리고 모든 상품이 단위 중량 당 동일한 가격을 갖는다고 가정하자. 목표는 총 중량이 W를 초과하지 않으면서 훔치는 상품들의 총 가격을 최대화하는 것이다.

  도둑에 대한 최적해는 총 무게가 W를 초과해서는 안된다는 제약 조건에 따라 총 무게를 최대화하는 물건들의 집합이다. 먼저 도둑은 총 무게가 W인 집합이 있는지 확인하려고 할 수 있다. 왜냐면 이것이 가능하다면 최적 해이기 때문이다. 어쨌든 이러한 집합을 결정하는 문제를 sum of subset문제라고 한다.

  일반화 해보자면 n개의 양의 정수들의 집합 S={w1, w2, ..., wn}와 양의 정수 W가 주어질 때, 합이 W와 같은 S의 모든 부분 집합을 찾는 것이다. 즉 합이 W인 모든 조합을 찾는 것이다. 예를 들어, S={1, 2, 5, 6, 8}, W=9 라면, {1, 2, 6}, {1, 8}이라는 해를 얻을 수 있다.

  주어진 집합 S의 요소들을 오름차순으로 정렬할 수 있다면 'w1<w2<...<wn'처럼 될 것이다. 만약 n의 값이 크다면 당연하겠지만 가능한 모든 조합을 검사하기에는 어려움이 있을 것이다. 따라서 백트래킹을 사용해야 한다. 그리고 인스턴스에 따라 해가 존재하지 않을 수도 있다.

  백트래킹을 사용하기 위해서는 가지치기를 위한 상태 공간 트리에서 유망한 노드를 고르는 promising function을 어떻게 해야할지 생각해야 한다. 일단 level i까지의 무게들의 총합을 \(U_i=w0+w1+...+w_i\)라고 하자. 그러면 나머지 무게들의 합을 \(R_{i+1}=w_{i+1}+w_{i+2}+...+w_n\)라고 할 수 있다. 그리고 T를 모든 무게의 합(\(w_0+w_1+...+w_n\))이라고 하자. 그리고 트리 탐색 전에 모든 무게를 오름차순으로 정렬한다고 가정하자. 그렇다면 유망하지 않을 두가지 경우를 설정할 수 있다.

• case 1: 만약 \(U_i+w_{i+1}>W\)라면, \(n_i\)는 유망하지 않은 노드이다. 왜냐하면 \(w_{i+1}\)는 남아있는 무게 중에서 가장 가볍기 때문이다. 즉 무게 총합이 너무 크다.
• case 2: 만약 \(U_i+R_{i+1}<W\)라면, 이후에 계속해서 트리를 확장해도 W를 얻을 수 없으므로 유망하지 않다.

위의 이유 중 하나로 유망하지 않은 경우를 정할 수 있고, 만약 \(U_i=W\)라면, 역추적을 하면서 해를 출력한다.

   우선 A={3, 5, 6, 7}, W=17이라는 인스턴스를 설정하고 백트래킹을 이용해 이를 해결해보자. 해결해보면 fig 3.1 같은 상태 공간 트리를 얻을 수 있을 것이다.

fig 3.1

각  노드들은 현재 상태까지의 부분합을 담고 있고, 부분집합은 각 노드까지의 경로로 표현할 수 있다. 전체 상태트리는 31개의 노드를 담고 있었어야 했는데, 여기서는 15개의 노드만을 확인하였다.

  이제 수도 코드로 표현된 알고리즘을 살펴보자. 가장 처음에는 Sum-of-Subsets(0, 0, total)을 호출해야 한다.

fig 3.1

Summary

1. 말단 노드에 해(W)가 담기지 않으면 W를 얻을 수 있는 남은 무게가 없기 때문에 유망하지 않다.
2. 1.을 바탕으로 \(u_i=W\)일 때, 재귀 호출이 종료되기 때문에 종료 조건 'i=n'이 확인되지 않을 수 있다.
3. 'i=n'일 때는 남은 무게가 없기 때문에 T=0이다.
4. \(u_i=W\)이면 OR 조건문의 두번째 조건이 평가되지 않기에 w[n+1]을 가질 수 없다.
5. 상태 공간 트리의 노드 개수는 \(2^0+2^1+...+2^n=(2^{n+1})-1\)
6. 만약 \(\sum_{i=1}^{n-1}w_i<W\)이고 \(w_n=W\)라면, 이 문제는 \(Z=\left \{w_n  \right \}\)라는 단 하나의 해만을 가진다.

 

Ex3. The 0-1 Knapsack Problem using backtraking

  동적 프로그래밍에서 해결해봤던 문제이다. 이번에는 백트래킹을 이용해서 이를 해결해보자. 우선 앞에서 본 sum-of-subset 문제와 달리 이 문제는 최적화 문제이다. 글의 처음에 잠깐 말했듯이 최적화 문제에서는 탐색이 끝날 때 까지 해를 알 수 없다. 생각해보자, 앞의 문제에서는 트리를 탐색하면서 부분집합의 정수 총합이 W라면 이를 해라고 할 수 있었지만 이 문제에서는 어느 단계까지 탐색하면서 얻은 부분집합의 합이 이 문제의 해라고 확정할 수 없다. 따라서 최적화 문제에 대한 백트래킹 알고리즘은 비최적화 문제와 약간의 차이가 있다.

  0-1 knapsack 문제에서는 노드 i까지 포함된 항목이 지금까지의 최적해보다 총 이윤이 더 크면 업데이트한다. 따라서 최적화 문제에서 우리는 항상 유망한 노드의 자식을 방문한다. 우선 최적화 문제를 위한 일반적인 백트래킹 알고리즘을 알아보자. fig 2.3과 큰 차이는 없으나 현재까지의 최적해보다 더 큰 값을 찾으면 최적해를 업데이트하는 것을 볼 수 있다.

fig 4.1

  그러면 가지치기를 위한 promising function에 대해 생각해보자. 유망하지 않은 노드를 판정할 수 있는 두가지 경우가 있다.

• case 1: (배낭에 있는 항목의 실제 총 무게) >= W일 때, \(u_i\)를 레벨 0에서 레벨 i까지의 총 무게라고 하자(\(u_i=w_0+w_1+...+w_i\)). 만약 \(u_i>W\)라면, 노드 i는 유망하지 않다(무게 제약). 만약 \(u_i=W\)라면, 노드 i는 유망하지 않다. 최적화가 되진 않았기 때문이다. 그러므로 만약 \(u_i \geq W\)라면, 해당 노드 i는 유망하지 않다.
• case 2: 만약 (실제 총 이윤) >= (각 물건의 무게당 가격을 참조했을 때의 이론적 한계)일 때 해당 노드는 유망하지 않다. 여기서 \(\frac {p_j}{w_j}\)(무게당 가격)이 큰 순으로 w[], p[]을 정렬하여 계산된다. 이 부분은 이해가 잘 잘 안됐으므로 더 살펴보자.
  • 이윤의 이론적 한계를 찾기 위해 현재 레벨 i에서 어디까지 내려갈 수 있을까? \(u_i\)를 레벨 0부터 i까지 선택한 물건들의 총 무게라고 하자. 그리고 레벨 i에서, 다음 두 조건을 만족하는 레벨 k만큼 내려간다고 하자.
    1. \(TW_{k-1} = w_{0}+w_{1}+...+w_{i}+w_{i+1}+...+w_{k-1}\leq W\)
    2. \(TW_{k-1}+w_{k} > W\)
  • 그리고 이론적 최대 이익 또는 한계를 추정해보자. 우리는 위에서 다음과 같은 관계를 얻을 수 있다. 그러니깐 이론적 한계는 총 무게가 W를 초과하게 될 때까지 물건을 계속 선택하고 남은 공간이 허용하는 만큼 마지막 물건의 일부분을 취하여 이를 마지막 물건 전까지의 이윤 총 합에 더하는 것이다.
    1. \(v_i = p_0+p_1+...+p_i\)
    2. TV_{k-1} = p_0+p_1+...+p_i+p_{i+1}+...+p_{k-1}\)
    3. \(bound = TV_{k-1}+(W-TV_{k-1})*\frac {p_k}{w_k}\)
  • 이렇게 얻어낸 bound 값이 지금까지 찾은 최적 해의 이윤 합보다 적다면 그 노드는 유망하지 않다.

  이를 바탕으로한 수도 코드를 확인해보자.

void knapsack (index i, int profit, int weight) {
	if (weight <= W && profit > maxprofit) { // 지금까지 최고의 답
		maxprofit = profit;
		numbest = i; 
		bestset = include; 
	}
    
	if (promising(i, profit, weight)) {
		include[i+1] = “YES”; // Include w[i+1]
		knapsack(i+1, profit+p[i+1], weight+w[i+1]);
		include[i+1] = “NO”; // Not include w[i+1]
		knapsack(i+1, profit, weight);
	}
}

  입력은 n, W, p[i]/w[i]의 내림차순으로 정렬된 배열 p[i], p[w]이고 출력은 maxprofit, numbest, bestset[], include[]이다. 첫번째 조건문을 만족한다면 해당 세트는 지금까지의 최적해이다. numberset을 해당 세트의 항목 수로 설정하고, 이 해를 이용해 bestset을 설정한다. 두번째 조건문은 i번째 물건이 유망하다면 i+1번째 물건을 택했을 때/택하지 않았을 때의 경우로 나눠서 상태 공간 트리를 확장한다.

bool promising(index i, int profit, int weight) {
	index j, k; 
	int totweight; 
	float bound;
	if (weight >= W) return FALSE;  //자식마디로 확장할 수 있을 때만 유망하다.
	else {							//자식마디에 쓸 공간이 남아 있어야 한다. 
		j = i+1;
	bound = profit; 
	totweight = weight;
	while ((j <= n) && (totweight +w[j] <= W)) {  //가능한 많은 아이템을 취한다. 
		totweight = totweight + w[j]; 
		bound = bound + p[j];
		j++
	}
	k=j;  		
	if (k <= n)  // k째 아이템의 일부분을 취함
		bound = bound +(W–totweight)*p[k]/w[k];
	
    return bound > maxprofit;
  }
}

  해당 코드는 유망 노드를 판별하는 코드이다. 해당 노드의 가격과 무게를 계산하고 그 노드의 bound를 계산한다. 만약 weight < W && bound > maxprofit이면 검색을 계속하고 그렇지 않다면 역추적한다.

 인스턴스를 하나 보자. n=4, W=16이고 각 물건에 대한 정보가 다음과 같을 때 fig 4.2와 같은 상태 공간 트리가 만들어진다.

fig 4.2

• note 1: 말단 노드는 bound 값이 이윤의 초기 값에서 변경될 수 없고 이는 이윤의 최대값보다 작기 때문에 유망하지 않다. 이것은 bound가 최대 이윤보다 클 수 없음을 의미한다. 결과적으로 promising function에서 i=n인 경우는 확인할 필요가 없다.
• note 2: bound값은 level k-1까지 왼쪽 경로를 따라 변경되지 않는다. 결과적으로 k번째 항목을 추가하면 가중치가 W보다 높기 때문에 이 노드의 왼쪽 노드는 유망하지 않다.
• note 3: 알고리즘은 다음 입력 인스턴스에 대해 worst-case()를 가지며 해는 n번째 항목만 사용한다.

  이제 시간복잡도를 알아보자. 동적 계획법에서는, wost-case 시간복잡도는 \(T(n)=O(nW, 2^n)\)이었다. 백트래킹 알고리즘에서 최악의 시간복잡도는 상태 공간 트리를 모두 탐색하는 것이므로 \(T(n)=O(2^n)\)이다. 그러나 이것은 백트래킹 알고리즘에서 최악의 경우 역추적을 통해 일반적으로 얼마나 많은 검사가 감소하는지에 대한 것이 거의 반영되지 않았기에 동적 계획법이 우수하다고 볼 수는 없다.

  이는 두 알고리즘의 상대적 효율성이 이론적으로 분석되기 어렵다는 것이다. 따라서 알고리즘을 여러 샘플 인스턴스에서 실행하고 일반적으로 더 나은 성능을 보이는 알고리즘을 확인하고 비교할 수 있을 것이다.

End

 일반적으로 백트래킹 알고리즘은 주어진 입력 인스턴스에 따라 결과가 다르다. 예를 들어 한 세트의 데이터로 0/1 배낭 문제를 해결할 때, 가지치기 없이 트리의 DFS를 완료해야 할 수도 있다. 그러나 다른 데이터 세트를 사용하면 같은 문제지만 대부분의 branch를 제거할 수도 있다.

---

자료 출처

• Introduction to The Design and Analysis of Algorithms / Ananu Levitin
• FOUNDATIONS OF ALGORITHMS / RICHARD E. NEAPORITAN
• Panda의 IT 노트 / https://seungjuitmemo.tistory.com/109