이전 글에서도 말했듯이 테이블 집합에 대한 쿼리(질의)는 결과로 relation(table)을 반환한다. 여기서는 관계 대수를 사용하여 각 쿼리를 표현할 것이다. 관계대수는 어떻게 쿼리를 수행할 것인가를 명시하는 절차적 언어이다. 이것은 SQL의 이론적 기초이다.
이 글에서도 이전 처럼 대학 원서 제출 서비스에서 발생하는 상황을 바탕으로 진행한다.
Query

Simplest query
가장 간단한 쿼리는 테이블 자체를 가져오는 쿼리이다. 표현도 단순하게 테이블 이름만 적으면 된다. 'Student'는 Studnet 테이블 자체를 가져오는 쿼리인 것이다. 여기에 연산자(operator)를 사용하여 필터링, 자르기, 병합 등의 작업을 수행할 수 있다.

Select operator
우선 특정 rows를 선택하는 연산자를 알아보자. 다음과 같은 형태를 가진다.
$$\sigma _{cond} Rel$$
'cond'에 특정 rows에 대한 조건이 들어가고 'Rel'은 relation의 이름이 들어간다. 이렇게 반환된 쿼리 결과에는 중복이 존재하지 않는다.
각 상황을 다음과 같은 관계대수로 표현할 수 있다.
- Students with GPA>3.7: \(\sigma _{GPA>3.7} Student\)
- Students with GPA>3.7 and HS<1000: \(\sigma _{GPA>3.7 \wedge HS>1000} Student\)
- Applications to Stanford CS major: \(\sigma _{CName = 'Stanford' \wedge major='cs} Student\)
Project operator
다음은 특정 columns를 선택하는 연산자이다. 다음과 같은 형태를 가진다.
$$\pi _{A_1,A_2, ...}Rel$$
\(A_1,A_2, ...\)에는 columns 이름이 들어가고 'Rel'에는 relation의 이름이 들어간다. 이 결과는 중복이 존재할 수 있다(예를 들어 점수나 전공이 같은 학생들이 있을 수 있으니깐). 그러므로 필요에 따라 이것을 없애줄 필요가 있다.
예를 들면 다음과 같다.
- ID and decision of all applications: \(\pi _{sID, dec}Rel\)
※ To pick both rows and columns
위에서 본 두 종류의 연산자를 적절히 조합하면 특정 rows들의 columns들만 뽑아낼 수 있다. 예를 들면 다음과 같다.
- ID and name of students with GPA>3.7
$$\pi _{sID, sName}\sigma _{GPA>3.7} Student$$
Cross Product operator

두 개의 relation들을 결합하는 연산자인 Cross Product(카디션 곱, x)에 대해 알아보자. 예를 들어 'R x S'면, R과 S의 튜플들의 모든 가능한 조합으로 이루어진 relation이다. 그렇기 때문에 카디션 곱의 결과 relation은 크기가 매우 클 수 있고, 실제로 사용자가 원하는 것은 해당 결과 relation의 일부인 경우가 대부분이므로 카디션 곱 자체는 유용한 연산자는 아니다.
- Names and GPAs of students with HS>1000 who applied to CS and were rejected
다음과 같은 상황이 있을 때 이를 관계대수로 표현하면 다음과 같다.
$$\pi _{SName, GPA}\sigma _{HS>1000 \wedge major='cs' \wedge dec='R' \wedge Student.sID=Apply.sID}(Student\times Apply) $$
이 연산의 결과 relation은 각 relation의 attributes가 합쳐진 8개의 attributes를 가지게 된다.
Join operator
조인 연산자는 두 개의 relations으로부터 연관된 튜플들을 결합하는 연산자이다. 위의 카디널 곱 연산자보다 더 유용하고 중요하다. 여러 종류의 조인 연산자가 있는데 몇가지 알아보자.
Theta Join
Theta Join(세타 조인, \(R\bowtie_{\theta}S\))의 결과는 카디션 곱에서 조건(\(\theta\))을 만족하는 튜플들로 이루어진 relation이다. 즉 세타 조인의 결과는 두 relation의 카디션 곱에 조인 조건을 적용한 결과와 동일하다.
$$ R\bowtie_{\theta}S \equiv \sigma_{\theta}(R\times S) $$
Equal Join
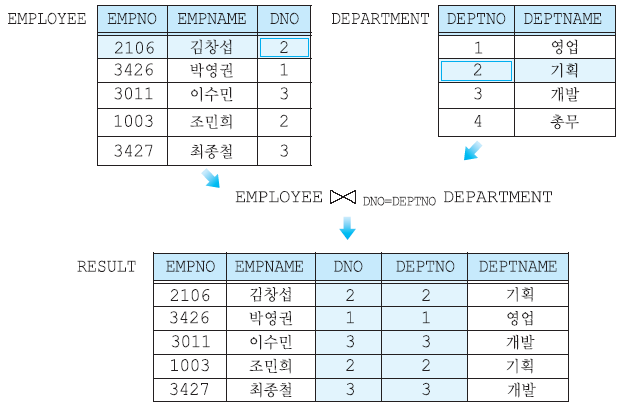
Equal Join(동등 조인, =)은 세타 조인 중에서 비교 연산자가 '='인 조인이다. fig 4를 보면 'DNO=DEPTNO'라는 동일한 정보가 중복되게 나오는 문제점을 발견할 수 있다.
Natural Join

Natural Join(자연 조인, *)은 두 relation의 공통된 attibutes에 대해 동등 조인을 수행하고 결과 relation에 있는 2개의 join attributes 중 하나를 제외한 조인이다. 동등 조인의 문제를 해결한 조인인 것이고 실제로 가장 자주 사용되는 조인 연산자이다.
Set operator
2개 이상의 relations에서 조인을 사용하지 않고 연관된 데이터를 조회하는 방법 중 하나이다. 이것을 사용하기 위해서는 두 relation이 합집합 호환이어야 한다. 여기서 합집합 호환의 필요 충분 조건은 두 relation R1(A1,A2,...,An)과 R2(B1,B2,...Bm)이 있을 때, n=m이고, 모든 1<=i<n에 대해 domain(Ai)=domain(Bi)이어야 한다.
Union operator(합집합 연산자, \(\cup\))
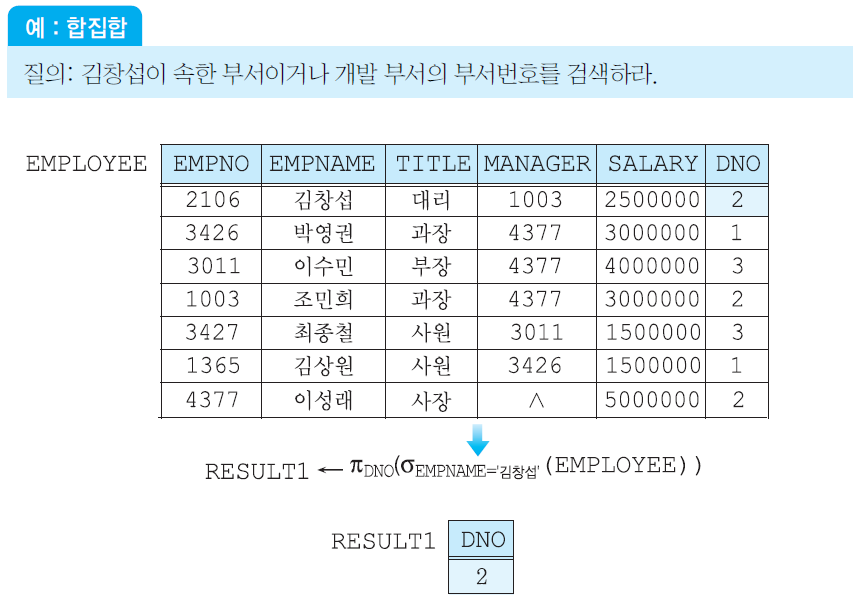
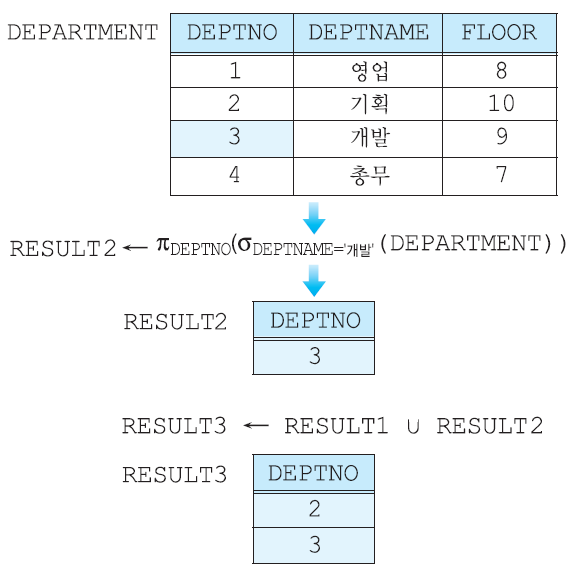
두 relation R과 S의 합집합이 있을 때 R ∪ S는 R또는 S에 있거나 R과 S 모두에 속한 튜플들로 이루어진 relation이다. 결과 relation에서 중복된 튜플들은 제외고, attributes의 이름들은 R이나 S의 attributes의 이름과 같다.
Intersection operator(교집합 연산자, ∩)
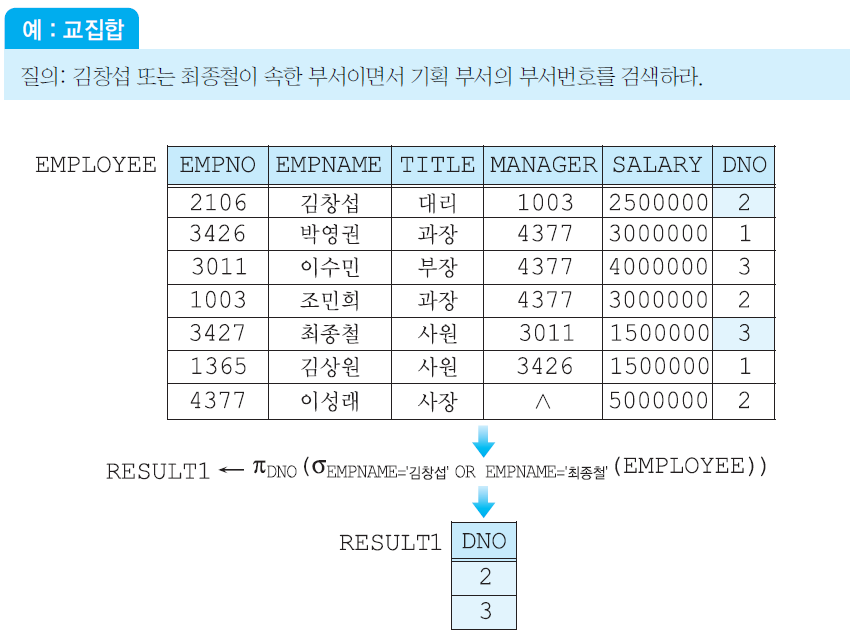
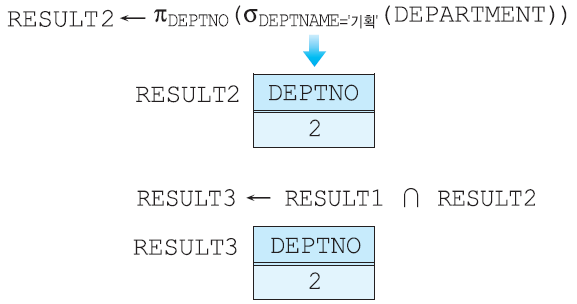
두 relation R과 S의 교집합 R ∩ S는 R과 S 모두에 속한 튜플들로 이루어진 relation이다. 결과 relation에서 중복된 튜플들은 제외고, attributes의 이름들은 R이나 S의 attributes의 이름과 같다.
Difference operator(차집합 연산자, -)
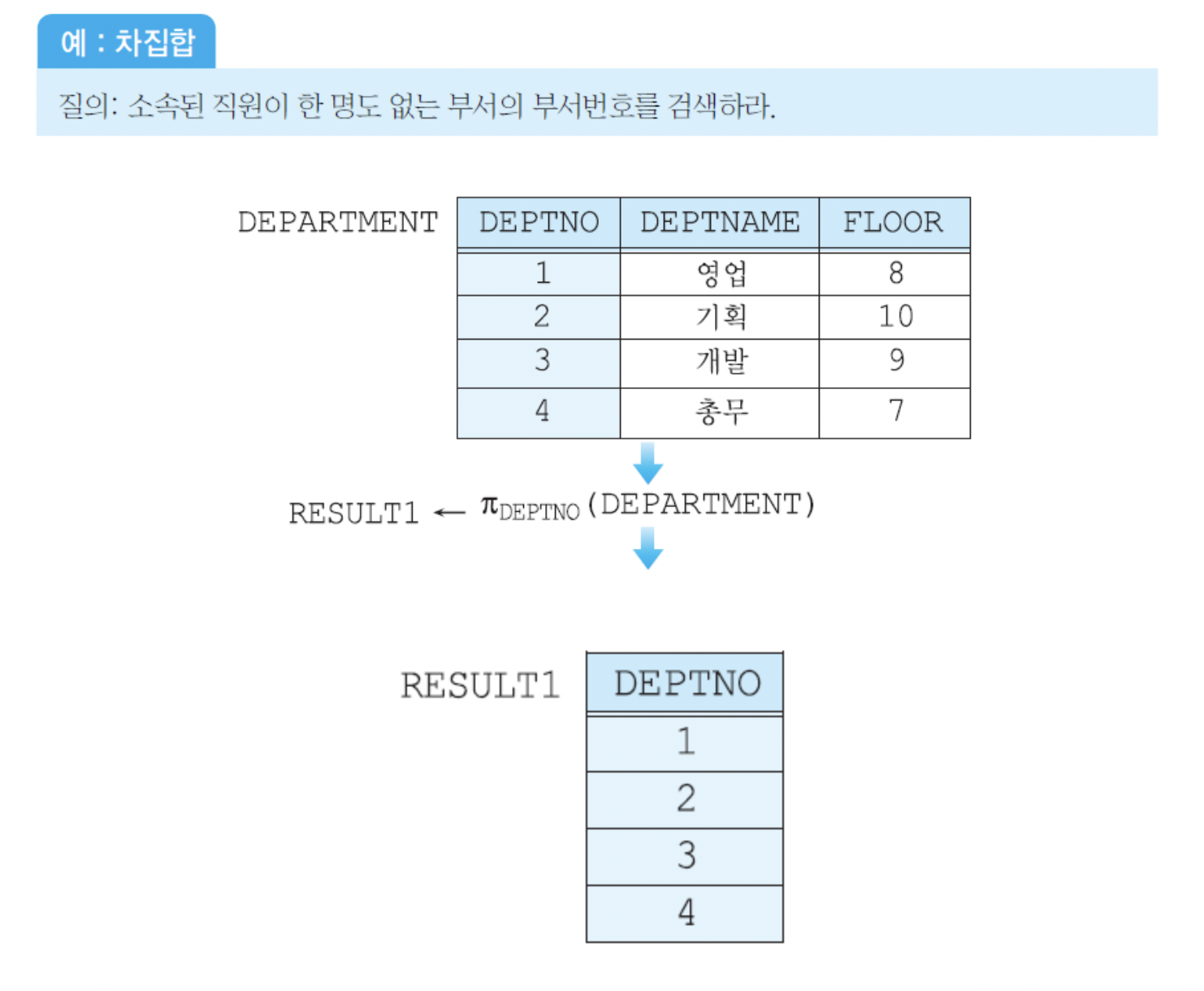

두 relation R과 S의 차집합 R-S는 R에는 속하지만 S에는 속하지 않은 튜플들로 이루어진 릴레이션이다. 결과 relation에서 중복된 튜플들은 제외고, attributes의 이름들은 R이나 S의 attributes의 이름과 같다.
※etc
- 중학교 때 배웠던 집합 공식을 이용하면 다음과 같은 관계를 확인할 수 있다.
- \(E_1 \cap E_2 \equiv E_1 - (E_1-E_2)\)
Rename operator(재명명 연산자, \(\rho\))
재명명 연산자는 \(\rho _{R(A1, A2, ..., An)}(E)\)의 형태를 갖는데 relation E의 이름을 R로 변경하고, attributes의 이름을 차례대로 A1, A2, ..., An으로 변경한다. relation의 이름만 바꾼다면 \(\rho_{R}(E)\), attributes만 바꾼다면 \(\rho_{A1,A2,...,An}(E)\)로 표현할 수도 있다.
자료참고
데이터베이스 4장 관계대수
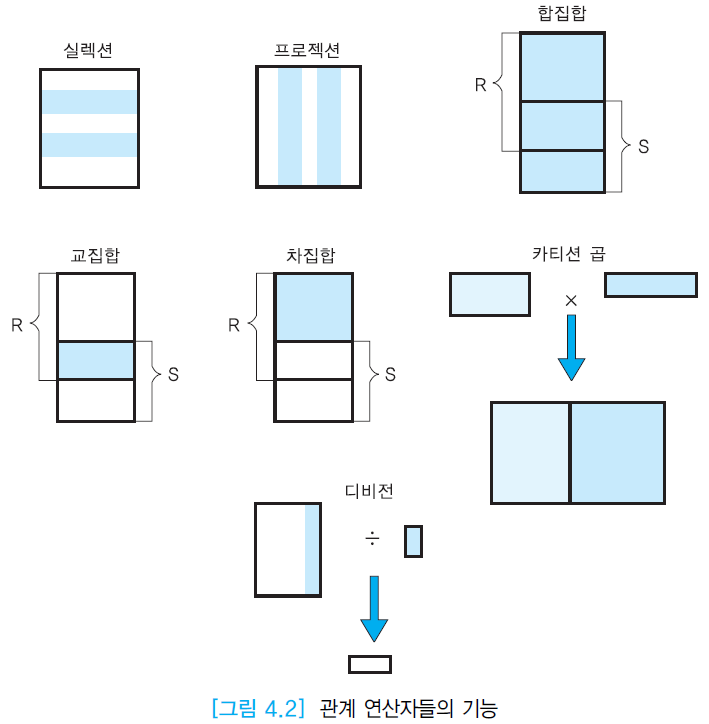
우린 관계 대수에 대해서만 알아본다. 관계 대수 관계 연산자를 통해 복잡한 관계 대수식을 만들 수 있다. 관계 연산자는 크게 두가지로 나눌 수 있다. 1. 실렉션 연산자 2. 프로젝션 연산자 예시
chopby.tistory.com
'Computer Science > 데이터베이스' 카테고리의 다른 글
| Relational design theory (0) | 2022.11.03 |
|---|---|
| SQL 3 (0) | 2022.09.28 |
| SQL 2 (0) | 2022.09.23 |
| SQL 1 (1) | 2022.09.19 |
| 관계 모델(Relational Model) (0) | 2022.09.12 |




댓글